用户定义的MPI派生类型

　　用户程序中的通信模式是程序中最难预测的部分。在很多情况下，用户需要进行对内存空间中非连续的数据进行发送，而且，为了减小通信开销，也需要有一种方法将多种不同类型的数据集中在一起进行发送，看下面的例子：

　　float a[1000]
　　发送 : a[5]-a[9]
　　　　　　MPI_Send(&a[5], 5, MPI_FLOAT,…..)
　　发送 : a[5],a[7],a[9],a[11],a[13],a[15]
　　　　　　for( i =5; i<16; i+=2 ){
　　　　　　　　MPI_Send(&a[i],1,MPI_FLOAT,….)
　　　　　　}
　　缺点: 多次发送，效率低，程序设计繁琐

　　对于前面讲到的通信方法，只讨论了如何把包含在同一缓冲区中具有相同数据类型的多个连续数据进行发送和接收，这对实际的应用程序显然是不够的。因此MPI提供了用户定义数据类型的能力，这就是对派生类型的支持。派生类型的概念与C语言中的结构类型的概念有一些相似。

　　对非连续/多类型数据进行传送的一种解决方法是在发送前将这些数据进行打包：先把它们都拷贝到一个连续的缓冲区中，然后在接收端再设法进行恢复。这种做法需要进行额外的内存操作，这会给通信系统的性能带来较大的问题。

　　要介绍MPI派生类型的定义，首先需要介绍类型图的概念。

　　任意一个MPI数据类型可以用两个n元组来描述，其中n为自然数。第一个n元组称为类型序列（type signature ），
　　　　Typesig = { type(0), type(1), ..., type(n-1) };

　　它用来描述构成这个数据类型的各元素的基类型，基类型可以是MPI的预定义数据类型，也可以是用户定义的派生类型，MPI的数据类型的定义采用这种嵌套定义的方法，可以很方便的定义出很复杂的数据结构；

　　第二个n元组称为偏移序列（ type displacements ），
　　　　Typedisp = { disp(0), disp(1), ..., disp( n-1) };

　　它用来描述数据类型的各元素相对于这个数据类型的起始位置的偏移（也就是各元素在类型图中的起始位置，可以参见下面的图）， 也称为基地址， 需要注意的是，这个偏移总是以字节为单位的，而且它可以为正，为零，也可以为负，数据类型中的各元素的偏移没有直接的联系。偏移序列中的偏移数不必是单调增的，这表明派生数据类型中的数据元素不要求是顺序排列的，由于偏移甚至可以为负，这时派生数据类型中的数据元素甚至可以出现在该派生数据的起始地址之前。

　　这两个n元组在定义派生数据类型的MPI函数中，会以数组的形式出现。

　　类型序列给出了数据类型的各组成元素的类型特征，而偏移序列则给出了各组成元素的位置特征，将类型序列和偏移序列中的元素一一配对就可以确定数据类型中的各组成元素，这个用于刻画数据类型的二元组序列称为该数据类型的类型图（type map ），它可以表示如下：
　　typemap = { ( type(0), disp(0) ), ( type(1), disp(1) ), ...,
　　　　　　　　( type(n-1), disp(n-1) ) };
　　类型图可以完整的刻画一个数据类型的属性。

　　假设具有该数据类型的数据的数据缓冲区的起始地址为buff，那么该数据类型中的第i个元素的起始地址为buff+disp(i)，类型为type(i)。

　　类型图不仅用来描述MPI的派生数据类型，也被用来描述MPI的预定义数据类型。通常情况下，MPI中预定义数据类型的类型图可以写成{(预定义数据类型，0)}，比如MPI_INTEGER的类型图为{(INTEGER, 0)}。

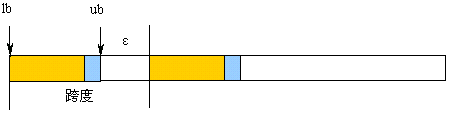
　　类型图的下界（ lowerbound ）定义为：
　　　　　　　　lb(typemap) = min{ disp(i) }, i = 0, 1, ...,n-1
　　
　　类型图的上界（ upperbound ）定义为：
　　　　　　　　ub(typemap) = max{ disp(i)+sizeof(type(i)) }, i = 0, 1, ...,n-1
　
　　类型图的跨度（ extent ）定义为：
　　　　　　　　extent(typemap) = ub(typemap) - lb(typemap) +ε

　　由于不同的类型有不同的地址对齐的要求，ε定义为使所有元素都能达到地址对齐要求时，下一个该类型的派生数据的起始位置也可以使它的各个元素满足地址对齐要求的最小非负整数值。

　　比如下面的例子：type_dc={(double, 0),(char, 8)}。如果double类型的地址对齐边界为8,那么这个数据类型的跨度为16。如下面的图。