|
归约
MPI_REDUCE( sendbuf, recvbuf, count, datatype, op, root, comm
)
IN sendbuf 发送缓冲区起始地址(待归约数据)
OUT recvbuf 接收缓冲区起始地址(root中存放最后结果的地址)
IN count 发送缓冲区中的数据个数(归约数组的长度)
IN datatype 归约的数据类型
IN op 归约操作类型
IN root 根处理器
IN comm 通信域
int MPI_Reduce( void *sendbuf, void *recvbuf, int count,
MPI_Datatype datatype, MPI_Op op, int root, MPI_Comm comm );
MPI预定义的归约操作类型如下:
|
归约操作
|
含义
|
允许的数据类型
|
|
C
|
|
MPI_MAX
|
最大值
|
整型,浮点型
|
|
MPI_MIN
|
最小值
|
整型,浮点型
|
|
MPI_SUM
|
和
|
整型,浮点型
|
|
MPI_PROD
|
积
|
整型,浮点型
|
|
MPI_LAND
|
逻辑与
|
整型
|
|
MPI_BAND
|
按位与
|
整型,字节型
|
|
MPI_LOR
|
逻辑或
|
整型
|
|
MPI_BOR
|
按位或
|
整型,字节型
|
|
MPI_LXOR
|
逻辑异或
|
整型
|
|
MPI_BXOR
|
按位异或
|
整型,字节型
|
|
MPI_MAXLOC
|
第一个最大值
|
专用类型
|
|
MPI_MINLOC
|
第一个最小值
|
专用类型
|
其中的整型包括:
MPI_INT MPI_UNSIGNED
MPI_SHORT MPI_UNSIGNED_SHORT
MPI_LONG MPI_UNSIGNED_LONG
浮点型包括
MPI_FLOAT
MPI_DOUBLE
MPI_LONG_DOUBLE
字节型为MPI_BYTE
专用类型是专门为这两个操作定义的,请参照MPI规范中对应的说明。
顺便提一句,除了这些预定义归约操作类型外,MPI允许用户自定义归约操作类型,对应的操作为MPI_OP_CREATE和MPI_OP_FREE。用户需要保证这个归约操作满足结合律,但不要求可交换性。
一个经典的例子。求π值。
这种方法所依赖的原理如下式:
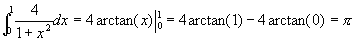
所以π值可以转化为求函数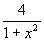 在[0,1]区间与x轴所夹图形的面积。可以用下面的公式来逼近这个面积: 在[0,1]区间与x轴所夹图形的面积。可以用下面的公式来逼近这个面积:
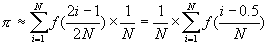
可以证明,通过增大N,可以以任意精度逼近π值。
程序如下(原例子由MPICH-1.2.3的例子cpi.c给出, /* */中为原文给出的注释
//后面的是本文中所加得注释,它们可以被安全的删除):
//pi.c
//使用mpicc -o pi pi.c进行编译
//使用mpirun -np 4 pi来运行(四个处理器)
#include "mpi.h"
#include <stdio.h>
#include <math.h>
// 计算出a点处函数f(x)=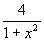 的值 的值
double f(double a)
{
return (4.0 / (1.0 + a*a));
}
int main(int argc,char **argv)
{
int done = 0, n, myid, numprocs, i;
//25位的PI的参考值
double PI25DT = 3.141592653589793238462643;
double mypi, pi, h, sum, x;
double startwtime = 0.0, endwtime;
int namelen;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc,&argv);
MPI_Comm_size(MPI_COMM_WORLD,&numprocs);
MPI_Comm_rank(MPI_COMM_WORLD,&myid);
MPI_Get_processor_name(processor_name,&namelen);
fprintf(stdout,"Process %d of %d
on %s\n",
myid, numprocs, processor_name);
n = 0;
while (!done)
{
if (myid == 0)
{
/*
printf("Enter the number of intervals: (0 quits) ");
scanf("%d",&n);
*/
//设定N值,注意,用上面的两个语句,可以由用户给出N值
if (n==0) n=10000; else n=0;
//进程0开始计时
startwtime = MPI_Wtime();
}
//由进程0广播N值
MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
if (n == 0)
done = 1;
else
{
//h是区间的步长
h = 1.0 / (double) n;
sum = 0.0;
/* A slightly better approach starts from large i and works back
*/
//注意每个处理器都通过myid来确定自己的工作。
for (i = myid + 1; i <= n; i += numprocs)
{
//x是每个区间的中点的x坐标
x = h * ((double)i - 0.5);
//sum现在包含的是每个处理器上的局部和
sum += f(x);
}
//得到了局部的面积,为了减少不必要的计算,从上面的循环中提了出来。
mypi = h * sum;
//由局部的面积得到总的面积
MPI_Reduce(&mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
//由进程0打印结果,误差和计算时间。
if (myid == 0)
{
printf("pi is approximately %.16f, Error is %.16f\n",
pi, fabs(pi - PI25DT));
endwtime = MPI_Wtime();
printf("wall clock time = %f\n", endwtime-startwtime);
fflush( stdout );
}
}
}
MPI_Finalize();
return 0;
}
|