1. 标准并行方法 (standard parallel approach)
　　这种并行方法的一个典型例子是由 T. C. Fogarty等[5]开发的一个基于共享存贮器方式
的并行遗传算法，该算法将全部群体存放在一个共享的存贮器中，各处理机并行评价各个个体的适应度。

　　2. 分解型并行方法 (decomposition parallel approach)
　　这种方法是将整个群体划分为几个子群体，各个子群体分配在各自的处理机或局域网工作站上独立地进行简单遗传算法的进化操作，在适当的时候各个子群体之间相互交换一些信息。其基本出发点是从全局的角度开发群体进化的并行性。这种方法改变了简单遗传算法的基本特点，各子群体独立地进行进化，而不是全部群体采用同一机制进化。它是实现上述第 4种并行性的方法，并且是一个简单常用、易于实现的方法。这种方法不仅能够提高遗传算法的运算速度，而且由于保持了各处理机上子群体进化的局部特性，还能够有效地回避遗传算法的早熟现象。构造这种并行遗传算法时，需要考虑下述几个主要问题：

　　● 子群体划分方式
　　整个群体均匀地分配到各个处理机的方式 (是粗粒度分配，还是细粒度分配？）。

　　● 交换信息方式
　　1. 参加信息交换的对象：哪几个处理机之间可以交换信息？
　　2. 交换信息的内容：是随机交换，还是择优交换？
　　3. 交换时间或频率：何时交换？
　　4. 交换信息量：交换几个个体？

　　根据对这几个问题的不同处理，构成了不同类型的群体交换模型，亦即形成了不同的并行遗传算法。

　　(1)步进模型 (stepping- stone model)
　　这个模型的各个子群体中所含个体的数量多于1，各个子群体在其处理机上并行独立地运行简单遗传算法，子群体之间的信息交换只能是在地理上的邻接处理机之间进行。该模型由于对处理机之间的通信要求不高，所以实现起来比较简单。图6.7.3步进模型的示例。
　　　　　　　　　　
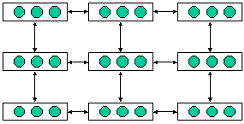
　　　　　　　　　　　　　　　图6.7.3 步进模型

R. Tanese[6]开发出的并行遗传算法就属于此种模型，算法中各处理机上的子群体独立地运行简单遗传算法，定期地选择优良个体复制到相互以超立方体的形式联接在一起的其它并行机上的子群体中。

　　(2)岛屿模型 (island morel)
　　这个模型也叫做粗粒度并行遗传算法 (coarse- grained PGA)。该模型每个处理机上子群体所含个体的数量多于 1，各个子群体在其各自的处理机上并行独立地运行简单遗传算法，并且随机的时间间隔、在随机选择的处理机之间交换个体信息。图6.7.4岛屿模型的示例。
　　　　　　　　　 　　　　
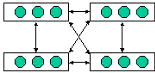
　　　　　　　　　　　　　　　　图6.7.4 岛屿模型

　　基于这种模型，B. Kroger等 [7]在有 32个处理机的并行机上开发了一个并行遗传算法用来解决二维装箱问题，算法中，各个处理机异步运行简单遗传算法，然后随机地将最佳的个体复制到其他处理机上，运行结果表明，这个方法比启发式的顺序算法性能上要好得多。

　　(3)邻接模型 (neighborhood model)
　　这个模型也叫做细粒度并行遗传算法 (fine- grained PGA)。该模型中每个处理机上只分
配一个个体，即子群体只由一个个体组成，每个子群体只和与其海明距离为 1的"邻接"子群体相互交换信息。由该模型的特点可知，即使群体中某一个体的适合度较高，其作用也仅仅是逐步地才能到其邻近的个体，所以它能够有效地维持群体的多样性，有效地抑制早熟现象。图6.7.5该模型的示例。
　　　　　　　
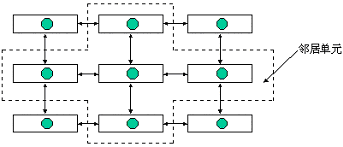
　　　　　　　　　　　　　　　　　图6.7.5 邻接模型

　　H. Tamiki[8]利用这种类型的并行遗传算法来解决生产车间的调度问题。E. G. Talbi等[9]也用这种类型的并行遗传算法解决图形划分问题。