遗传算法的并行通常有三种模式：同步主从式、异步主从式和网格式，如图6.7.1所示。我们对它的研究可分为主从式模型、粗粒度模型和细粒度模型3种[3]。主从式模型只是对适应度的计算进行了并行化；粗粒度模型是将群体划分成若干子群体独立演化，并以一定间隔在子群体之间交换个体，它有集中式迁移和阶梯式迁移两种主要的迁移模式；细粒度模型将群体划分成数目较多的子群体，每个子群体的个体数较少，个体迁移通过子群体之间部分重叠的方式进行。并行遗传算法引入了"迁移"这个新的操作 ,它的作用是以一定的迁移率和迁移间隔在各子群体之间交换个体，迁移率是每次交换个体的数目，迁移间隔是相邻两次迁移之间的时间间隔。
　

　


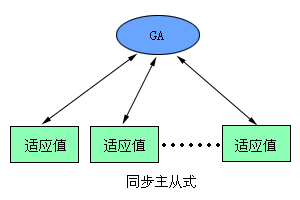
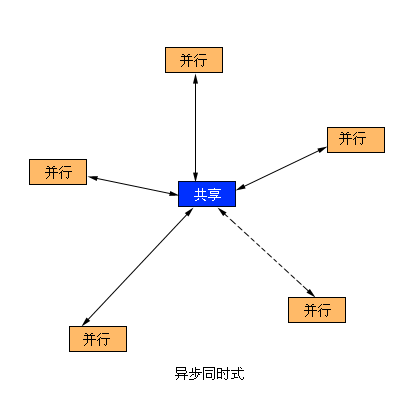
　　　　　　　　　图6.7.1　粗粒度并行遗传算法的并行模式

　　D. E. Goldberg[4]归纳出了基本遗传算法模型 (Simple Genetic Algorithm,简称 SGA),它是一个反复迭代的进化计算过程，通过对一组表示候选解的个体进行评价、选择、交叉、变异等操作，来产生新一代的个体 (候选解)，这个迭代过程直到满足某种结束条件为止。对应于基本遗传算法的运行过程，为实现其并行化要求，如图6.7.2所示，可以从下面四种并行性方面着手对其进行改进和发展。 　　　　　　　　　

图6.7.2 遗传算法的并行机制

　　● 并行性1 个体适应度评价的并行性
　　个体适应度的评价在遗传算法中占用的运行时间比较大。通过对适应度并行计算方法的研究，可提高个体适应度评价的计算效率。

　　● 并行性2 整个群体各个个体适应度评价的并行性
　　群体中各个个体适应度的评价过程无相互依赖关系，这样各个个体适应度的评价或计算过程就可以相互独立、相互并行地在不同的处理机上同时进行。

　　● 并行性3 子代群体产生过程的并行性
　　从父代群体中产生下一代群体所需进行的选择、交叉、变异等遗传操作可以独立并行地进行。

　　● 并行性4 基于群体分组的并行性
　　群体中的单个或一组个体的进化过程可以相互独立地进行，在适当的时候，它们再以适当的方式交换信息。即不同个体或不同组个体的进化过程是同时进行的。

　　在上述四种并行方式中，前三种方式并未从总体上改变简单遗传算法的特点，第四种并行方式却对简单遗传算法的结构有较大的改变，并且这种方式也最自然，在并行机或局域网环境下实现起来也最简单，所以受到了人们较大的重视。目前已开发出的并行遗传算法基本上都是基于上述四种并行机制或其组合来实现的。