遗传算法（Genetic Algorithm，缩写为GA）是一种有效的解决最优化问题的方法。它借用了生物遗传学的观点，通过自然选择、遗传、变异等作用机制，实现各个个体的适应性的提高。这一点体现了自然界中"物竞天择、适者生存"进化过程。它最先是由John Holland[1]于1975年提出的，从那以后，它逐渐发展成为一种通过模拟自然进化过程解决最优化问题的计算模型、最优化问题通常可归结为极大化问题，利用数学公式描述就写作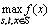： 其中f(x)为目标函数，Ｓ为可行域，它们是由工程实际问题的具体条件决定的。

　　利用遗传算法解最优化问题，首先应对可行域中的点进行编码（一般采用二进制编码），然后再可行域中随机挑选一些编码组成作为进化起点的第一代编码组，并计算每个解的目标函数值，也就是编码的适应度。接着就像自然界中一样，利用选择机制从编码组中随机挑选编码作为繁殖过程前的编码样本。选择机制应保证适应度较高的解能够保留较多的样本；而适应度较低的解则保留较少的样本，甚至被淘汰。在接下去的繁殖过程中，遗传算法提供了交叉和变异两种算子对挑选后的样本进行交换。交叉算子交换随机挑选的两个编码的某些位，变异算子则直接对一个编码中的随机挑选的某一位进行反转。这样通过选择和繁殖就产生了下一代编码组。重复上述选择和繁殖过程，直到结束条件得到满足为止。进化过程最后一代中的最优解就是用遗传算法解最优化问题所得到的最终结果。

　　用遗传算法解决问题时，首先要对待解决问题的模型结构和参数进行编码，一般用字符串表示，这个过程就将问题符号化、离散化了。也有在连续空间定义的GA(Genetic Algorithm in Continuous Space, GACS)。

　　一个串行运算的遗传算法(Seguential Genetic Algoritm, SGA)按如下过程进行：
　　① 对待解决问题进行编码；
　　② 随机产生一个由确定长度的特征串组成的初始群体X(0):=(x1, x2, … xn)；
　　③ 对当前群体X(t)中每个个体xi计算其适应度F(xi)，适应度表示了该个体的性能好坏；
　　④ 应用选择算子产生中间代Xr(t)；
　　⑤ 对Xr(t)应用其它的算子，产生新一代群体X(t+1)，这些算子的目的在于扩展有限个体的覆盖面，体现全局搜索的思想；
　　⑥ t:=t+1；如果不满足终止条件继续③
　
　　GA中最常用的算子有如下几种：
　　● 选择算子(selection/reproduction): 选择算子从群体中按某一概率成对选择个体，某个体xi被选择的概率Pi与其适应度值成正比。最通常的实现方法是轮盘赌(roulette wheel)模型。
　　● 交叉算子(Crossover): 交叉算子将被选中的两个个体的基因链按概率pc进行交叉，生成两个新的个体，交叉位置是随机的。其中Pc是一个系统参数。
　　● 变异算子(Mutation): 变异算子将新个体的基因链的各位按概率pm进行变异，对二值基因链(0,1编码)来说即是取反。

　　上述各种算子的实现是多种多样的，而且许多新的算子正在不断地提出，以改进GA的某些性能。系统参数(个体数n,基因链长度l,交叉概率Pc,变异概率Pm等)对算法的收敛速度及结果有很大的影响，应视具体问题选取不同的值。

　　从以上介绍可以看出，GA算法具有下述特点：
　　・GA是对问题参数的编码组进行进化，而不是直接对参数本身。
　　・GA的搜索是从问题解的编码组开始搜索，而不是从单个解开始。
　　・GA使用目标函数值（适应度）这一信息进行搜索，而不需导数等其他信息。
　　・GA算法使用的选择、交叉、变异这三个算子都是随机操作，而不是确定规则。

　　实践表明，遗传算法解最优化问题的计算效率比较高、适用范围相当广。为了解释这一现象，Holland给出了图式定理。所谓图式，就是某些码位取相同值的编码的集合。图式定理说明在进化过程的各代中，属于适应度高、阶数低且长度短的图式的编码数量将随代数以指数形式增长。另外，Holland还发现遗传算法具有隐含的并行计算特性。最近的研究则表明，上述遗传算法经适当改进后对任意优化问题以概率１收敛于全局最优解。

　　近年来，随着对于遗传算法研究的不断深入完善，有越来越多的人认识了解了遗传算法，并把它应用到越来越广泛的领域，例如机器学习、模式识别、图像处理、神经网络、工业优化控制和社会科学等方面。特别是在解决旅行商问题、煤气管道的最优控制、通信网络链接长度的优化问题、铁路运输计划优化、喷气式飞机涡轮机的设计、VLSI版面设计、键盘排列优化等问题上遗传算法都取得了很大的成功。

　　将遗传算法用于解决各种实际问题后，人们也发现遗传算法也会由于各种原因过早向目标函数的局部最优解收敛，从而很难找到全局最优解。其中有些是由于目标函数的特性造成的，例如函数具有欺骗性，不满足构造模块假说等等；另外一些则是由于算法设计不当。为此，不断有人对遗传算法提出各种各样的改进方案。例如：针对原先的定长二进制编码方案，提出了动态编码、实数编码等改进方案；针对按比例的选择机制，提出了竞争选择、按续挑选等改进方案；针对原先的一点交叉算子，提出了两点交叉、多点交叉、均匀交叉等算子；针对原先遗传算法各控制参数在进化过程中不变的情况，提出了退化遗传算法、自适应遗传算法等。另外，针对不同问题还出现了分布式遗传算法、并行遗传算法等等。

　　本文主要讨论并行遗传算法。在解决复杂问题时 ,若用串行的 GA模拟群体的进化求出全局最优解 ,需要花费大量计算时间。为了大大提高搜索效率 ,需要对 GA进行并行处理 ,这也是GA研究的一个重要方向。在文章的后面，综述了各种并行遗传算法的构成原理，介绍了其典型应用情况，并指出了需进一步研究的课题。