|
并行Floyd算法
设处理器个数为p,可以把D(k)划分到p个处理器上,通过并行计算其各个元素的值来完成并行化。作为一个矩阵,D(k)有多种划分方式,这里只讨论分块棋盘划分。
利用分块棋盘划分,D(k)划分为p个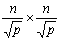 的矩阵块并分别分配给p个处理器。在第k次迭代中,每个处理器Pij都需要矩阵第k行和第k列的元素来完成计算,因此保存有第k行和第k列元素的处理器需要分别在列方向和行方向进行1到多的广播,把数据传送给同列(或同行)的其它 的矩阵块并分别分配给p个处理器。在第k次迭代中,每个处理器Pij都需要矩阵第k行和第k列的元素来完成计算,因此保存有第k行和第k列元素的处理器需要分别在列方向和行方向进行1到多的广播,把数据传送给同列(或同行)的其它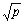 个处理器。当处理器采用超立方体互联结构并采用切通路由(Cut-Through
Routing)方式进行通信时,把 个处理器。当处理器采用超立方体互联结构并采用切通路由(Cut-Through
Routing)方式进行通信时,把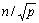 个元素广播给 个元素广播给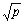 个处理器处理器需要花费 个处理器处理器需要花费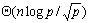 的时间。每次迭代时各个处理器需要一个同步操作,这需要花费时间 的时间。每次迭代时各个处理器需要一个同步操作,这需要花费时间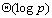 。每次迭代每个处理器上计算n2/p个元素的值所花费的时间是 。每次迭代每个处理器上计算n2/p个元素的值所花费的时间是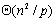 。因此整个并行处理时间(即n次迭代所花费的总时间)为: 。因此整个并行处理时间(即n次迭代所花费的总时间)为:
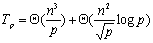
其中第一项是计算时间,第二项是通信时间。由于串行处理时间为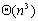 ,因此并行算法的加速比和效率分别为: ,因此并行算法的加速比和效率分别为:
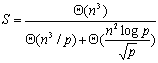
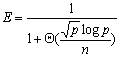
|