|
Floyd算法利用动态规划思想(见下一节),通过把问题分解为子问题来解决任意两点见的最短路径问题。设G=(V, E, w)是一个赋权图,其边V={v1,
v2, …, vn}。对于k≤n,考虑其结点V的一个子集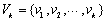 。对于V中任何两个结点vi、vj,考虑从vi到vj的中间结点都在vk中的所有路径,设 。对于V中任何两个结点vi、vj,考虑从vi到vj的中间结点都在vk中的所有路径,设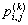 是其中最短的,并设 是其中最短的,并设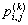 的路径长度为 的路径长度为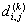 。如果结点vk不在从vi到vj的最短路径上,则 。如果结点vk不在从vi到vj的最短路径上,则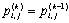 ;反之则可以把 ;反之则可以把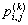 分为两段,其中一段从vi到vk,另一段从vk到vj,这样便得到表达式 分为两段,其中一段从vi到vk,另一段从vk到vj,这样便得到表达式 。上述讨论可以归纳为如下递归式: 。上述讨论可以归纳为如下递归式:

原问题转化为对每个i和j求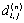 ,或者说求矩阵 ,或者说求矩阵 。 。
利用上述递归表达式,串行Floyd算法可以写成图6.6.8的样子。算法包括三个循环,每个循环需要运行步骤n,最内部的循环体可以在常数时间内完成,因此算法的复杂度为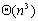 。 。
串行Floyd算法
|