|
算法的并行化
最直观的并行化方式是利用n个处理器,每个处理器取图中不同的结点独立地运行Dijkstra算法,这种方式叫做源分割法(Source-Partitioned
Formulation)。另外一种方法是每一步的Dijkstra算法都在各个处理器上并行完成,这叫做源并行法(Source-Parallel
Formulation)。
源分割法比较简单,因为各个处理器之间无需进行任何通信,独立地进行计算即可。并行处理时间就是Dijkstra算法的串行处理时间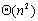 。算法的加速比和效率分别是: 。算法的加速比和效率分别是:
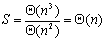
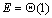
当处理器个数不多时,这种方法是很好的选择,但其缺点是处理器个数最多只能为n。
源并行法与源分割法类似,只不过并行处理部分放在Dijkstra算法本身了,性能也差不多。
当处理器个数p>n时,把p个处理器分成n组,每组p/n个处理器。每组处理器并行运行一个Dijkstra算法,n组刚好完成对应于n个不同结点的Dijkstra算法。即把源分割与源并行相结合。这样最多可以利用n2个处理器。
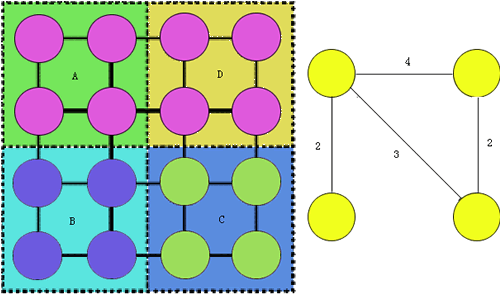
图6.6.7 源分割与源并行结合来完成任意两点间最短路问题的并行化
处理器互联结构为二维网格,n=4,p=16
设p=q2个处理器互联成二维网格结构(见图6.6.7),并设q是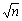 的整数倍。这样,q×q的网格被分成了n个子网格,每个子网格拥有 的整数倍。这样,q×q的网格被分成了n个子网格,每个子网格拥有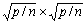 个处理器,每个子网格负责完成一个结点的Dijkstra算法(见练习题)。则整个算法的并行处理时间为: 个处理器,每个子网格负责完成一个结点的Dijkstra算法(见练习题)。则整个算法的并行处理时间为:
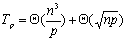
其中第一项是计算时间,第二项是通信时间。这样,算法的加速比S和效率E可以表达如下:
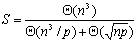
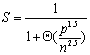
可见,混合法要优于源分割法与源并行法。
|
