|
矩阵相乘法的核心思想是通过n次迭代,第k次迭代得到任意两个结点间边的条数最多为k时的最短路径。图采用赋权邻接矩阵的存储结构,邻接矩阵的各个元素实际上是两个结点间直接连线的权重。设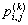 是从结点vi到vj的最短路,前提是路径最多包含k条边;并设 是从结点vi到vj的最短路,前提是路径最多包含k条边;并设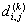 是 是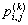 的长度。设 的长度。设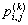 的倒数第二个结点是vm,则有: 的倒数第二个结点是vm,则有: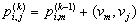 。这样得到下面的递推式: 。这样得到下面的递推式:
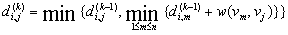
又因为结点到自己的最短路径为0,因此上式简化为:
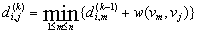
设D(k)=(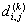 ),因为G任意两点之间的最短路径不会超过图的边数(否则会出现环,必不为最短),因此D(n-1)为问题的解。在上面的递归表达式中,如果把加法看成乘法,把求最小值看成加法,则形式上等同于矩阵相乘,即形式上可以表达为: ),因为G任意两点之间的最短路径不会超过图的边数(否则会出现环,必不为最短),因此D(n-1)为问题的解。在上面的递归表达式中,如果把加法看成乘法,把求最小值看成加法,则形式上等同于矩阵相乘,即形式上可以表达为:
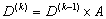
这样,问题就转化为利用特殊的加法和乘法求An-1。利用折半乘法(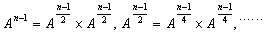 )可以只需要进行logn次矩阵乘法运算,见图6.6.6。由于每次矩阵乘法运算需要 )可以只需要进行logn次矩阵乘法运算,见图6.6.6。由于每次矩阵乘法运算需要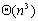 的时间(这里仅仅考虑最简单的矩阵相乘算法,而不考虑快速算法),因此整个串行算法的时间复杂度为 的时间(这里仅仅考虑最简单的矩阵相乘算法,而不考虑快速算法),因此整个串行算法的时间复杂度为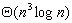 。 。
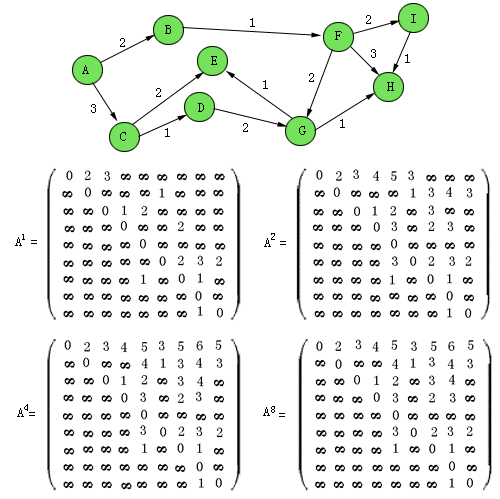
图6.6.6 用矩阵自乘法求任意两点间最短距离的演示
|