对于一个无向图G，满足如下三个条件的图T称为G的支撑树（Spanning Tree）：
　　1) T是G的子图；
　　2) T是一棵树（无环连通图）；
　　3) T包含G的所有结点；

　　定义一个赋权图的权为其所有边的权之和。则图G的最小支撑树（Minimum Spanning Tree，简称MST）定义为权最小的支撑树或称为最短树。只有连通图才存在最小支撑树，并且有限连通图一定存在最小支撑树。最小支撑树问题是图论的基本问题之一。图6.6.3是一个图及其最小支撑树的例子。
　　　
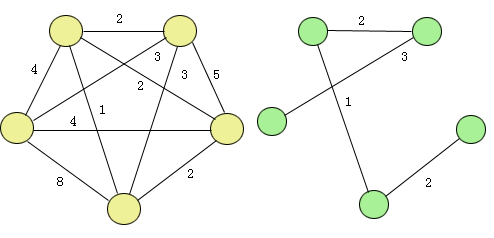
　　　　　　　　　　图6.6.3 一个无向图和它的最小支撑树

　　有很多求最短树的算法，比较经典的有Kruskal算法和Prim算法。