图 一个图G可以表示为一个二元组（V, E），其中V和E分别是结点和边的有限集合。图可以分为有限图与无限图，一般研究感兴趣的是有限图。在下面的讨论中，如果没有特殊说明，就认为V={v1, v2, …, vn}，E={e1, e2, …, em}，即结点数|V|=n，边数|E|=m。

　　图的边 图G的边可以是有方向的，也可以是无方向的，分别称为有向边和无向边，连接两个结点vi和vj的边e记为(vi, vj)，此时称两个结点称为相邻结点。如果e为无向边，则两个结点称为边的两个端点；如果时有向边则两个点分别称为始点和终点。两个结点之间可以有多条边。

　　度 与图的某结点v关联的所有边数称为结点的度，记为d(v)。对于有向边，以v为起点的边数之和称为v的正度，记为d⁺(v)；以v为终点的边数之和称为v的负度，记为d^－(v)。关于度有一些简单的性质：
　　√ 任何一个图G中所有结点的度之和等于边数的两倍；
　　√ 任何一个图G中度为奇数的结点为偶数个；
　　√ 任何一个有向图（定义见下）中正度之和等于负度之和。

　　子图 给定图G=(V, E)和G'=(V', E')，如果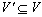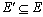，，则称G'为G的子图（Subgraph）。如果G'是G的子图且包含了G的所有顶点，则称G'为G的支撑子图或生成子图。如果G'是G的子图且包含了包含了图G在V'之间的所有边，则称为G的导出子图。

　　图的路径 对于图G和一个序列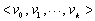，如果序列中每个元素都是图G的结点，且序列中相邻两个元素所对应的结点之间都有边相连，则此序列称为图G中从v0到vk的一个路径（Path）。如果图G的两个结点u和v之间有一个路径，则称从u可以到达v。如果路径上的结点各不相同，则称为简单路径。如果路径的起点和终点相同，则称为环。如果环的内部结点各不相同，则称为简单环。

　　图的分类 如果图G的所有边都是无向边，则称为无向图；如果所有边都是有向边则称为有向图；既包含有向边又包含无向边的图称为混和图。本节只研究有向图和无向图。图中所有结点之间都有边相连的图叫完全图。如果图G中任何两个结点u和v之间都有存在路径，则称为连通图（Connected Graph）。如果图G中不存在环，则称为森林（Forest）；连通的森林称为树（Tree）。

　　有关图的更多信息，请参见清华大学出版社出版的《图论与代数结构》（戴一奇等编著）。