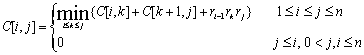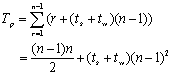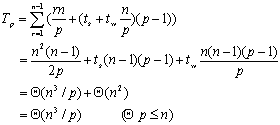所谓矩阵乘积的运算次序问题，是指多个矩阵的乘积A₁×A₂×......×A_n 按照怎样的运算次序（即怎样加括号）使得运算速度最快的问题。根据矩阵运算的结合性，不论按照怎样的次序运算，其结果都是一样的，但运算速度有所不同，现举例来说明。比如要计算乘积A₁×A₂×A₃，假设三个矩阵的大小分别为5×10、10×20和20×40。按照(A₁×A₂₎×A₃的运算次序所花的操作步数是5×10×20＋5×20×40＝5000；而按照A₁×(A₂×A₃₎的运算次序所花的操作步数是10×20×40＋5×10×40＝10000。后者所花的时间是前者的两倍。看来寻找一个合适的运算次序是很有必要的。

　　最简单的方法是穷举法，把所有可能的情况一一列举出来，计算其时间开销，从中选出耗时最少的运算次序。设有n个矩阵参与相乘，需要进行n-1次乘法运算，这些运算之间的次序共有(n-1)!种，这是指数增长的，扩展性很差。

　　用动态规划的思路来解决问题。设C[i, j]是矩阵乘积A_i×A_i+1.....×A_j的最优操作步数，把它看成两个矩阵的乘积：(A_i×A_i+1.....×A_k )×(A_k×A_k+1.....×A_j)，则有：
　　　　　　　　　　　　
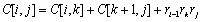
　　其中矩阵Ai的规模为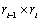。由于C[i, j]仅可以由不同的k而得到，因此得到下面的递推公式：
　　　　　　　　　　　　
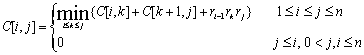
　　整个问题转化为求C[1, n]。同样把不同的C[i, j]组织成一个矩阵，但由于i≤j时C[i, j]的值为0，因此实际构成一个上对角阵，见图6.5.4。考察矩阵各个元素之间的依赖关系，并画出依赖关系图，可以发现，依赖关系图是一个有向无环图，即不存在循环依赖的情况。事实上，每个元素只依赖于本行和本列中序号比自己小的元素，因此跟上面各个问题一样，可以通过行方向、列方向和对角线方向来顺次计算，只要保证每一行或每一列都是按照序号从低到高的顺序即可。从图6.5.4可以看到，对角线上n-1个元素的计算时间为1，距离对角线距离越大，计算时间越长，与对角线距离为k的n-k-1个元素其每个元素的计算时间为k+1。因此整个串行计算时间为：
　　　　　　　　　　　　
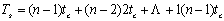
　　根据数学知识可知。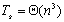
　　　　
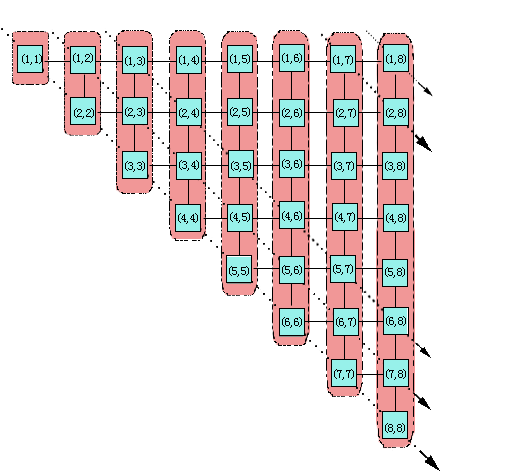
　　　　　　　　　　图6.5.4 矩阵乘积的运算次序问题

　　考虑在n台处理器所构成的环状结构上的并行处理时间。计算过程n步，在第r步，计算距离对角线r+1的元素的值，每个处理器完成一个值的计算。矩阵元素在各个处理器上的划分见图6.5.4。在完成每一步的计算后，每个处理器都把自己的计算结果发送到其它所有的处理器，以便在下一次迭代时每个处理器都可以直接从本地内存获取数据。考虑第r次迭代需要花费的时间，由于元素依赖于r个其它元素，因此本元素值的计算需要花费r的时间，计算结果广播所花费的通信时间是（t_s+t_w）（n-1），因此第r次迭代所花费的总时间为（r+（t_s+t_w）（n-1））。整个处理时间为：
　　　　　　　　　
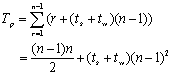
　　可见并行处理时间的量级为。因为串行处理时间为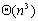，并且处理器数目为n，因此此并行算法是成本最佳的。

　　类似地，可以用p（p<n）台处理器来解决问题，只不过每台处理器要完成矩阵多列（n/p）元素的计算，第r次迭代的计算时间为nr/p。在每次迭代中同样需要把本次计算的结果广播到其它的处理器，广播所需要的时间是(t_s+t_wn/p)(p-1)。因此并行处理时间为：
　　　　　　　　　　　
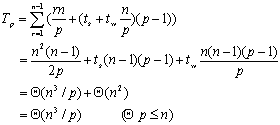
　　并行算法的成本为：
　　　　　　　　　　　　
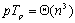
　　可见算法是成本最佳的。