|
在阐述最长公共子串问题之前,先给出几个定义。
序列的长度 序列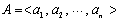 中的元素个数n称为序列的长度或称为序列的秩,记为|A|。 中的元素个数n称为序列的长度或称为序列的秩,记为|A|。
子序列(Subsequence) 给定一个序列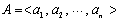 和另一个序列B,如果从A中删除一些元素后能够得到B,则称B为A的子序列,记为 和另一个序列B,如果从A中删除一些元素后能够得到B,则称B为A的子序列,记为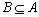 。 。
公共子序列(Common-Subsequence) 设A、B、C为三个序列,如果C既是A的子序列,又是B的子序列,则称C为A和B的公共子序列。
最长公共子序列(Longest-Common-Subsequence) 设A、B为两个序列,S(A, B)为两个序列的公共子序列的集合,即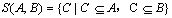 ,则S(A,
B)中长度最大的序列定义为两个序列A、B的最长公共子序列。 ,则S(A,
B)中长度最大的序列定义为两个序列A、B的最长公共子序列。
此外,把序列A的前j个元素所构成的子序列记为Aj,A的第j个元素记为A[j]。
比如序列<a, b, f>是序列<a, b, c, d, e,
f>的子序列,但不是<a, f, b, d>的子序列。两个序列<a, b, c, d, e, f>和<a,
e, h, k, c, z, f>的所有公共子序列如下:
<a>、<c>、<e>、<f>、
<a, c>、<a, e>、<a, f>、<c, f>、<e,
f>
<a, c, f>、<a, e, f>
其中<a, c, f>和<a, e, f>是最长公共子序列。
用动态规划法解决两个序列A、B的最长公共子序列问题,可以定义函数F[i, j]表示A的前i个元素所构成的子序列与B的前j个子串所构成的子序列的最长公共子序列的长度。这样求A、B的最长公共子序列就是求F[|A|,
|B|]。动态规划递推表达式如下:
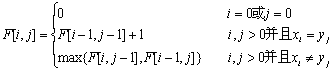
上述递推式可以这样解释:假设F[i-1,j-1] 、F[i-1,j] 、F[i,j-1]均为已知,来求F[i,j]。考虑序列A的第i个元素A[i]和B的的j个元素B[j],A[i]=B[j]时,则必然有F[i,j]=F[i-1,j-1]+1,否则如果有F[i,j]-F[i-1,j-1]>1,则把Ai与Bj的最长公共子序列去掉最后一个元素后成为Ai-1与Bj-1的最长公共子序列,矛盾。当A[i]≠B[i]时,Ai与Bj的最长公共子序列Cij不可能既包含A[i]又包含B[j](否则意味着A[i]=B[j])。如果Cij不包含A[i],则
;而如果Cij不包含B[j],则F[i,j]=F[i,j-1],当然,有可能F[i,j]=F[i-1,j]=F[i,j-1],此时Cij即不包含A[i]又不包含B[j]。
(a) (b)
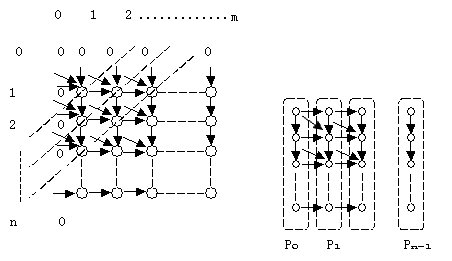
图6.5.3 (a) 最长公共自序列问题的求解矩阵;(b) 矩阵元素到处理器的映射
所有的F[i, j]构成了一个矩阵,见图6.5.3,计算矩阵中所有元素的值即给出了问题的解。先考虑串行算法,本问题中F[i,
j]的计算不仅依赖于前一列的元素,而且依赖于前一行的元素,在这方面比上两个问题要复杂。考虑到F[i, j]只依赖于上一行的元素以及本行中列序号比自己低的元素,因此可以按照行方向来计算,每行从最低列序号开始算起。考虑到F[i,
j]只依赖于上一列的元素以及本列中行序号比自己低的元素,因此还可以按照列方向来计算,每列从最低行序号开始算起。另一种计算次序是按照对角线来算,即按照如下次序:
F[0,0], F[0,1], F[1,0], F[0,2], F[1,1], F[2,0], ……
不论按照何种次序,计算一个元素所花的时间都是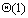 ,完成整个求解过程所花的时间为 ,完成整个求解过程所花的时间为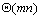 。 。
来考虑在CREW PRAM体系结构上的并行化,不妨设m≤n,并设采用m个处理器。这m个处理器每个负责计算m列中的一列,由于元素计算的依赖关系(见图6.5.3),计算的迭代进度是从矩阵的左上向右下而不是平行于列而进行的,这样需要的迭代次数是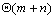 。又因为每步迭代过程只需要 。又因为每步迭代过程只需要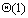 的时间,因此并行处理时间为 的时间,因此并行处理时间为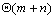 。并行算法的成本是 。并行算法的成本是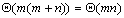 ,可见算法是成本最佳的。 ,可见算法是成本最佳的。
|