|
设有一个容量为c的背包和n个编号分别为1到n物体,设物体i的重量和效用指数分别是整数wi和pi。定义向量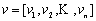 为背包状态。所谓0/1背包问题就是求背包状态
,使得 为背包状态。所谓0/1背包问题就是求背包状态
,使得
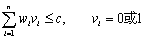
并且使下式的值为最大
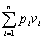
通俗地说,背包问题就是把n个物体中的若干个塞进背包,使得重量不超过一定的界,并且物体的效用指数之和最大。
当vi可以取除了0和1之外的其它值时,问题仍然属于背包问题,但不是0/1背包问题。所谓一维背包问题,是指物体只有一个约束条件:重量。如果有多个约束条件则称为多维背包问题。
解决背包问题最简单的方法是穷举法,即比较所有可能的2n中情况,找出满足重量约束条件并且效用指数之和最大的一种情况。这种方法的最大缺点在于其时间的指数增长率。下面将会看到,使用动态规划法可以在当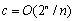 时得到较低的指数增长率,c越小则问题解决的时间复杂度越优于穷举法。 时得到较低的指数增长率,c越小则问题解决的时间复杂度越优于穷举法。
设F[i, x]为用i个对象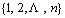 填充容量为x的箱子的背包问题的解,则F[n,
c]为问题的解。背包问题的动态规划递归表达式为: 填充容量为x的箱子的背包问题的解,则F[n,
c]为问题的解。背包问题的动态规划递归表达式为:
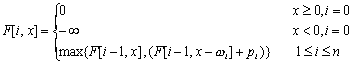
简单地解释一下上面的式子:对于F[i, x],如果其中包含了对象i,则F[i, x]可以表达为:
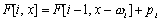
如果没有包含对象i,则F[i, x]可以表达为:
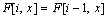
取二者中的较大者(因为得到最大效用)得到上面的递推式。
根据上面的递推式,可以构造一个n×c的矩阵F来存放F[i, x](其中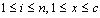 ),见图6.5.2。由于每一行的计算都依赖且只依赖于下面一行中的两个元素(而不依赖于同行的元素),因此按照行来逐次计算矩阵各个元素的值比较方便。由递推式可以知道,矩阵每一行中每个元素的计算都只需要O(1)的时间,因此串行计算整个矩阵所花的时间是O(nc)。 ),见图6.5.2。由于每一行的计算都依赖且只依赖于下面一行中的两个元素(而不依赖于同行的元素),因此按照行来逐次计算矩阵各个元素的值比较方便。由递推式可以知道,矩阵每一行中每个元素的计算都只需要O(1)的时间,因此串行计算整个矩阵所花的时间是O(nc)。
再考察在c个处理器(P0到Pc-1)的CREW PRAM并行体系结构上的并行化。每个处理器计算矩阵的一列(只所以不是每个处理器计算一行,理由同串行的情况),计算过程分n次迭代。在第j次迭代中,计算第r行的处理器Pr-1需要知道F[j-1,
r]和F[j-1, r-wj] 的值。由于是共享内存的体系结构,处理器可以在O(1)时间内取到任何元素的值,并在O(1)时间内把结果计算出来,这说明每次迭代需要单位时间。因此总的并行处理时间为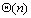 。类似可以知道,在CREW
PRAM体系结构上p(P≤n)个处理器的并行处理时间为 。类似可以知道,在CREW
PRAM体系结构上p(P≤n)个处理器的并行处理时间为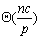 。 。
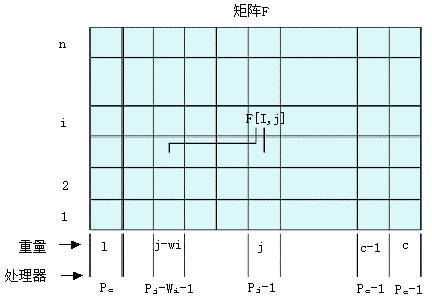
图6.5.2一维0/1背包问题的子问题划分和求解
当c个处理器互联成一个超立方体结构时,假设每个处理器都在自己的本地内存中保存有每个对象的重量与效用指数,并且处理器Pr上要完成F[j,
r+1](1≤j≤n)的计算。计算F[j, r]需要F[j-1, r] 和F[j-1, r-wj],其中F[j-1, r]存在本地内存中,而F[j-1,
r-wj]则需要通过处理器之间的通信来获取。在超立方体上采用切通路由(Cut-Through Routing)完成这些通信操作需要的时间是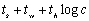 。设单个处理器上每次迭代所花的时间是
,则考虑到通信后每次迭代所花的时间是: 。设单个处理器上每次迭代所花的时间是
,则考虑到通信后每次迭代所花的时间是: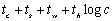 。因此解决整个问题(n次迭代)的并行处理时间为 。因此解决整个问题(n次迭代)的并行处理时间为
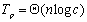
总成本为:
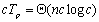
可见,当处理器个数p=c时,超立方体上的上述并行算法不是成本最佳的(即并行成本的量级高于串行成本)。
在超立方体体系结构中,当处理器个数p<n时,每个处理器要计算矩阵多列的值,每个处理器上的计算时间为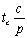 。计算通信时间时注意到每个处理器所需要的矩阵元素可能来自于两个远程处理器,因此通信时间至多为( 。计算通信时间时注意到每个处理器所需要的矩阵元素可能来自于两个远程处理器,因此通信时间至多为(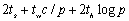 )。因此n次迭代所花的总时间是 )。因此n次迭代所花的总时间是
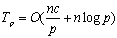 。 。
总成本为:
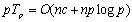
当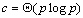 时,并行成本等于串行成本。可见上述算法的可扩展性不错。 时,并行成本等于串行成本。可见上述算法的可扩展性不错。
|