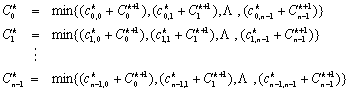|
考虑图6.5.1所示的无向图,它有r+1层,中间各层每层有n个结点,最边缘的两层(第0层和第r层)各有一个结点,每层所有结点都跟下一层所有结点有道路相连。第0层的结点S和第r层的结点R分别称为起点和终点。目标是求从起点到重点的最短路。为了便于说明问题,先介绍一些符号表示。第k层的第i个结点表示为vik;连接结点vik和vjk+1的道路的长度定义为ci,jk;从任何一个结点vik到终点R的最短路记为cik;对于第k层的n个结点,向量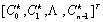 记为Ck。这样问题可以表示为求C0,即求 记为Ck。这样问题可以表示为求C0,即求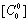 。 。

图6.5.1 最短路问题图示,一个r+1层的无向图
利用动态规划的思想,把问题分解为一系列子问题,要求第k层的某结点vik到终点R的最短路,因为最短路必然经过第k+1层的某个结点vjk+1
,这样,结点vik到终点R的路程等于从结点vik到vjk+1的路程加上从vjk+1到R的路程。得到下面的递归表达式:

显然又有:
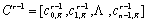
利用上面的两个式子可以递推得到C0。
因为递推式中只含有一个不同的递推项,因此这是一个一维动态规划问题。
把上面Cik的表达式展开可以得到:
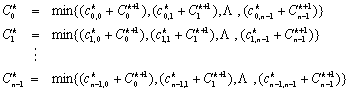
可以看到,上式与矩阵向量相乘的从形式上看很像。实际上,把上式中的加法运算替换为乘法运算,把求最小值的运算替换为加法运算,则上面的式子变为矩阵相乘,即:
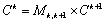
其中Ck和Ck+1都是n×1的向量,Mk,k+1是一个n×n的矩阵,其元素M[i,j]存放从第k层第i个结点到第k+1层第j个结点之间的道路长度,如下:

这样,就把问题转化为矩阵向量相乘的问题,当然,"乘法"和"加法"都是假的,但这并不影响计算复杂度的分析。
在单台处理器上计算每层的最短路向量Ck需要花费 的时间,串行解决整个问题(r层)的时间复杂度为 的时间,串行解决整个问题(r层)的时间复杂度为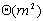 。 。
当p(P≤n)个处理器并行执行时,由6.3节并行稠密矩阵运算可知,完成每层最短路向量的计算需要 的时间,因此并行解决整个问题的时间复杂度为 的时间,因此并行解决整个问题的时间复杂度为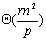 。特别地,当处理器个数p=n时,整个问题可以在 。特别地,当处理器个数p=n时,整个问题可以在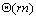 时间内完成。 时间内完成。
当图6.5.1中相邻两层的各个结点之间只有少数有直接的道路相连时(即其它结点之间的道路长度都为无穷大),上面的矩阵Mk,k+1为稀疏矩阵。借助6.4节所讲述的稀疏矩阵与向量乘积的并行化方法,有望在更低的时间复杂度内完成问题的求解。
总之,最短路问题可以通过虚拟加法与乘法运算的方式转化为矩阵与向量乘积的问题,从而利用现成的方法加以并行化。
|