|
动态规划把一个问题看成一系列相互关联的子问题,子问题再分成更小的问题,小的子问题的解决导致大子问题的解决,最终解决整个问题。设问题r分解成t个子问题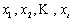 ,则问题r的解f(r)可以表示为: ,则问题r的解f(r)可以表示为:
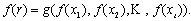
其中g称为组合函数,它依赖于问题本来的性质。对于优化问题,g常常为取最大值或最小值。当g取最大值或最小值时,把此方法称为动态规划法。典型的能够用动态规划法解决的问题包括最短路问题、背包问题、调度问题、模糊串匹配问题等。
动态规划根据不同的标准可以进行不同的分类。当上面的表达式中只包含一个递归项时,称为一维动态规划(Monadic Dynamic
Programming);而当表达式中含有多于一个递归项时则称为多维动态规划(Polyadic Dynamic Programming)。
各个子问题之间的依赖关系可以用一个有向图来表示,如果子问题P1依赖于子问题P2,则从P1向P2连一条线。如果这样构成的有向图是一个非循环图(即图中找不到一个点,使得从此点出发沿着有向边最终能够回到起点),则整个图可以分成若干等级,使得每一级子问题只依赖于前面的若干等级。对于有些动态规划问题,每一级子问题只依赖于其紧接着前面的一级;而有些问题的某一级子问题要依赖于前面的很多级。
鉴于线性规划问题的种类繁多性,很难给所有的线性规划问题给出一个通用的并行化解决方案。但一个问题的并行化往往能够带动一系列问题的解决。本节分析几个常见动态规划问题的并行算法,希望能够以此解决几类而不是所有动态规划问题的并行化问题。
|