利用图分割来实现可扩展的并行算法

　　下面来讨论借助于平面无向图来处理一类特殊稀疏矩阵与向量的乘法。设一个n×n的稀疏矩阵A具有对称结构，即如果A[i, j]非零，则A[j, i]也非零。可以根据这种对称矩阵生成一个关联图G，生成方式如下：

　　1) 图G的定点数目等于矩阵A的行数（和列数）。
　　2) 如果矩阵元素A[i, j]非空，则在图G的定点i和j之间连一条边。

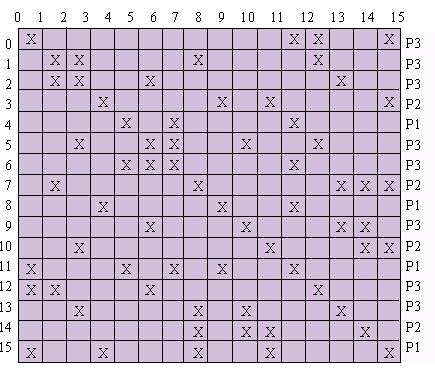
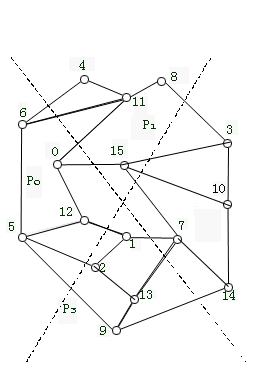
　　一个稀疏对称矩阵和它的关联图见图6.4.11。
　　

(a)

(b)

　图6.4.11 一个16×16的不规则稀疏矩阵和它的关联图
　　　　(a) 稀疏矩阵；(b) 关联图及其划分

　　当一个稀疏矩阵的关联图是平面图时，存在可扩展的矩阵向量相乘算法。所谓平面图，直观地讲，是指图可以画在一个平面上，使得各个边之间不产生交叉。注意，图的平面性是矩阵向量乘法可扩展的充分而非必要条件。

　　如果关联图是平面图，则可以把图的各个结点划分到各个的处理器上。选择合适的划分使得处理器间的通信尽可能少，就可以尽可能提高算法的性能。

　　直接寻找关联图的最佳划分是一个比较难的问题。不过从具体问题本身常常隐含了比较好的划分方式。

　　有关利用关联图来解决矩阵运算的详细情况，请查阅相关资料。