|
利用棋盘分割来提高性能
现在尝试一下棋盘分割。请注意,对原稀疏矩阵M而不是其值矩阵V和列序号矩阵J进行棋盘分割。设处理器个数为p=q2,则最初每个处理器上存储一个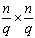 的矩阵块。与6.3节类似的推理可以得到在超立方体体系结构上切通路由所花通信的时间大约为: 的矩阵块。与6.3节类似的推理可以得到在超立方体体系结构上切通路由所花通信的时间大约为:
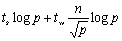
设非零元素在矩阵M中均匀分布,则每个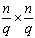 的矩阵块中大约含有 的矩阵块中大约含有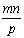 个非零元素,因此每个处理器在计算阶段平均要花费tc 个非零元素,因此每个处理器在计算阶段平均要花费tc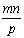 的时间。当然,这仅仅是一个平均时间,实际比这要多一些,取决于非零元素分布的均匀性,为了简单起见,假设分布足够均匀以至于计算的时间量级不会发生变化。这样,整个并行处理时间为: 的时间。当然,这仅仅是一个平均时间,实际比这要多一些,取决于非零元素分布的均匀性,为了简单起见,假设分布足够均匀以至于计算的时间量级不会发生变化。这样,整个并行处理时间为:
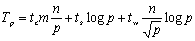
算法的加速比为:
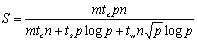
算法的效率为:
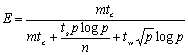
本算法尽管性能(从加速比和可扩展性来看)仍然不尽人意,但比前一算法要好。
|