一个简单的并行算法：条带状分割

　　对于矩阵的行向存储格式，一个简单的并行化方式是把值矩阵V和列序号矩阵J按照分块条带状划分并分配到p个处理器上，每个处理器上分配n/p行，mn/p个元素。向量X也同样均匀地分配到p个处理器上，每个处理器存放n/p个元素。
　　　
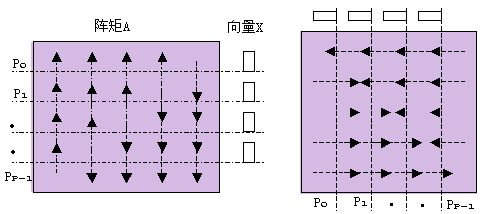
　　　　　　　　　(a) 　　　　　　　　　　　　　　　　　(b)
　　　　　　　图6.4.10 不规则稀疏阵与向量相乘的数据通信过程
　　　(a) 行方向条带划分时的多对多通信；(b) 列方向条带划分时的多对多通信

　　对于每个处理器，要计算矩阵某行与向量的乘积，必须获得与矩阵此行非零元素对应的各个向量元素。由于在不规则稀疏阵中，非零元素出现的列是随机的，任何一列都可能非零，因此每个处理器都需要得到向量的所有元素。这就需要一个多对多广播的过程，见图6.4.10。广播通信阶段之后就可以进行计算了，计算阶段所花的时间是t_cmn/p。通信阶段的时间与底层网络互联结构有关，假设为超立方体结构，则多对多广播所花费的时间是。因此总的并行处理时间为：
　　　　　　　　　　

　　从上式可以看到并行处理时间为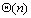，与串行处理时间为同一个量级，即并行化并没有引起渐进性能的提高。造成这种现象的主要原因在于多对多通信消耗了太多的时间。那么列向条带状划分会不会提高性能呢？类似的分析可以知道：不会。