|
并行化方案二:循环条带状分割
接下来的几段内容探讨通过循环条带状分割来提高并行处理性能的可能性。先从一个具体的例子来说明问题。假设稀疏矩阵的大小为36×36,要利用9个处理器来完成并行处理。把矩阵的行序号(0-35)排列成一个6×6的矩阵,见图6.4.9。现在来研究这6×6=36行如何分割并映射到9个处理器上。按照图6.4.9,把此行序号矩阵进行块棋盘划分,并把原矩阵中的各个行按照此行号的划分而分配到相应的处理器上。向量也按照元素的序号做同样的划分。可以验证,利用这种方式对原矩阵进行的循环条带状划分能够保证将来进行矩阵向量乘积运算时通信只在相邻的处理器之间进行。
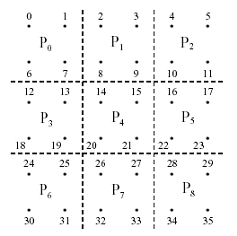
图6.4.9 一个36×36的分块三对角稀疏矩阵的行序号矩阵以及其棋盘分割
一般情况下,对于一个n×n的矩阵,可以构造一个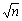 × ×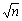 的行序号矩阵,并将其进行棋盘划分,然后根据棋盘划分的结构把原矩阵的每一行映射到相应的处理器上,结果是每个处理器上分配的n/p行实际上是由 的行序号矩阵,并将其进行棋盘划分,然后根据棋盘划分的结构把原矩阵的每一行映射到相应的处理器上,结果是每个处理器上分配的n/p行实际上是由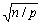 组连续的行构成的,每组有 组连续的行构成的,每组有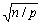 行,相邻两个行组之间的间距是 行,相邻两个行组之间的间距是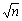 。可以证明,这样划分的好处是在矩阵与向量乘法运算中每个处理器只需要与其相邻的4个处理器进行通信。 。可以证明,这样划分的好处是在矩阵与向量乘法运算中每个处理器只需要与其相邻的4个处理器进行通信。
整个并行计算过程可以分为两个步骤,第一个步骤每个处理器与其周围的处理器通信以交换数据,因为只有边界数据需要交换,因此通信时间可以控制在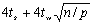 内,而不论底层是网格还是超立方体互联结构。第二步每个处理器内部独立进行乘法和加法运算,时间为5tcn/p。总的处理时间是: 内,而不论底层是网格还是超立方体互联结构。第二步每个处理器内部独立进行乘法和加法运算,时间为5tcn/p。总的处理时间是:
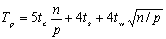
算法的效率为:
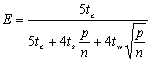
从并行处理时间和效率的表达式可以看出,这种循环条带状分割比块条带状分割的效果要好。
|