|
并行化方案一:矩阵条带状分割
先考虑一个简单直接的并行化方案:矩阵条带状分割,参见图6.4.8。假设处理器数目为p,这样n×5的矩阵按照行方向条带状分割后每个处理器上有5n/p个矩阵元素和n/p个向量元素。对于处理器上的每一个向量元素,要在进行乘积运算,处理器必须获得此向量元素对应行的5个矩阵元素。按照这5个元素所在的对角线分情况讨论。主对角线上的元素与对应的同一行的向量元素已经在一个处理器上,不用做额外的工作。对于紧靠主对角线的两个对角线上的元素,与对应的行上的向量刚好错了一位,但由于每个处理器上有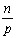 行,所以总有 行,所以总有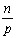 -1行是对的,所以每个处理器只需要向其相邻(左邻居或右邻居)传送一个矩阵元素。每个对角线需要的通信时间是ts+tw。 -1行是对的,所以每个处理器只需要向其相邻(左邻居或右邻居)传送一个矩阵元素。每个对角线需要的通信时间是ts+tw。
再来考虑剩下的两条对角线上的元素,这是最复杂的一种情况。与对紧靠主对角线的两个对角线元素的分析类似,剩下两个对角线上的元素需要移动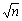 位。分两种情况讨论:n/p≥ 位。分两种情况讨论:n/p≥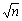 和n/p< 和n/p<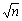 ,即p≤ ,即p≤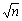 和p>
和p>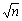 。当n/p≥ 。当n/p≥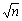 时,对于每条对角线,只需要每个处理器把矩阵的 时,对于每条对角线,只需要每个处理器把矩阵的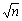 个元素发送给相邻的处理器即可,所花费的时间是ts+tw 个元素发送给相邻的处理器即可,所花费的时间是ts+tw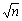 。当n/p< 。当n/p<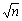 时,源处理器和目标处理器不再相邻,而是距离为p/ 时,源处理器和目标处理器不再相邻,而是距离为p/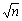 。当底层的网络互联结构为超立方体时,这种通信需要花费的时间是ts+twn/p+thlogp。 。当底层的网络互联结构为超立方体时,这种通信需要花费的时间是ts+twn/p+thlogp。
现在可以在各个处理器上并行地进行乘法和加法运算了,设单位乘法和加法运算需要花费tc的时间,则计算部分所花费的时间是5tcn/p。
综合考虑通信和计算,整个并行处理时间Tp可以分情况表达为:
当p≤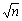 时, 时,
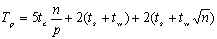
当p>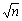 时, 时,
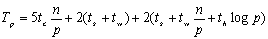
简单讨论一下算法的效率和可扩展性。当p≤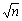 时,从上面的表达式可以看到并行算法的成本 时,从上面的表达式可以看到并行算法的成本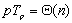 ;而当p> ;而当p>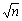 时: 时:
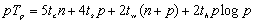
从上式可以看到,维持成本为O(n)只需要plogp≤n。可见算法的可扩展性比较好。
当p>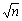 时,算法的效率为: 时,算法的效率为:
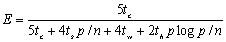
可以看到,效率不会超过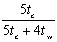 ,可见当通信延迟比较大时,算法的效率较低。 ,可见当通信延迟比较大时,算法的效率较低。
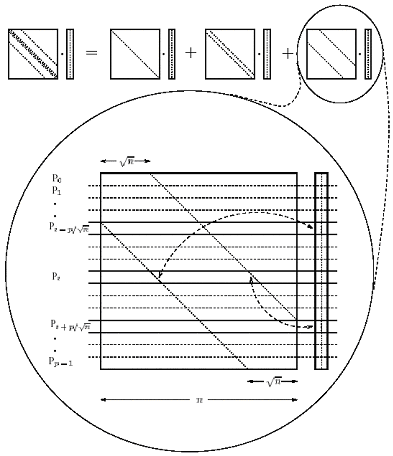
图6.4.8 分块三对角矩阵条带状分割时的矩阵向量乘积
|