|
向量X、Y内积的串行计算比较简单,只需把X[i]与Y[i]对应相乘,然后把结果相加即可,复杂度为O(n)。
当并行执行时,设处理器个数为p,参与计算的两个向量在分别每个处理器上放置n/p个元素。整个计算过程分为两步:第一步,各个处理器独立地进行乘积和加法运算,时间为n/p;第二步,各个处理器之间进行结果累加,在超立方体上需要消耗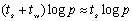 的时间。总的时间为: 的时间。总的时间为:
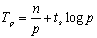
类似地,在二维网格互联结构中所消耗的时间为:
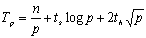
当两个向量为稀疏向量时,由于向量可以看作特殊的矩阵,因此上一小节所讲述的稀疏矩阵存储格式对稀疏向量同样实用,并且因为向量只有一维,稀疏存储格式将变得很简单,并且不同的矩阵存储格式用于向量可能会退化成同一种。以下的讨论假设采用坐标存储格式,由于向量只有一维,因此用两个向量(一个值向量和一个索引向量)而不是三个便可以存储稀疏向量的信息。以下设两个向量非零元素的个数分别为m、k,不失一般性设m≥k。
两个稀疏向量X、Y内积的算法见图6.4.6,很容易知道其复杂度为O(m+k)。在p个处理器上并行计算时,X的m个非零元素分布在p个处理器上,平均每个处理器拥有m/p个元素。Y的k个非零元素可以根据X非零元素的序号分配到p个处理器上面。

图6.4.6 稀疏向量内积的串行算法
|