坐标存储格式采用三个等长的一维数组来存储矩阵信息，数组长度等于矩阵非零元素的个数。具体来说，设一个稀疏矩阵有q个非零元素，则三个数组的长度是q的数组中：

　　√ 第一个数组V（Value的所写）存放矩阵的各个非零元素的值；
　　√ 后两个数组I（行方向）和J（列方向）分别存放非零元素的行坐标和列坐标（不妨假定坐标值从0开始）。
　　图6.4.1演示了一个6×6的稀疏矩阵以及其坐标存储格式。
　　　
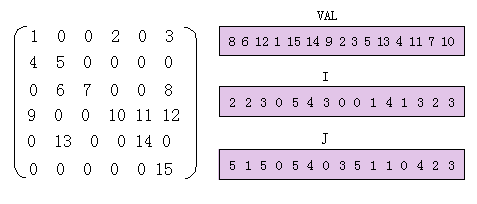
　　　　　　　　(a) 　　　　　　　　　　(b)
　　　　　　图6.4.1 一个6×6的稀疏矩阵以及其坐标存储格式
　　　　　　　　　(a) 稀疏矩阵；(b) 坐标存储格式

　　下面来分析一个坐标存储格式的空间占用情况。设稀疏矩阵的行数和列数分别为r和c，非零元素数目为q；设一个矩阵元素值所占用的存储空间为f（一般为32或64位）；一个矩阵行列值索引所占的存储空间为d（一般为16或32位）。则普通存储方式所占用的空间为：
　　　　　　　　　
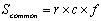
　　坐标存储格式所占用的存储空间为：
　　　　　　　　　
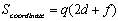
　　假设f=2d，则可以知道，当矩阵中非零元素的个数小于所有元素个数的1/2时，采用坐标存储格式能够节省存储空间。