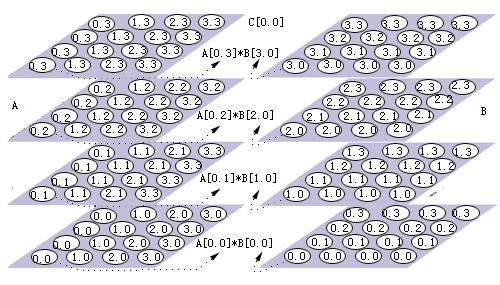|
本小节所介绍的DNS算法能够在p(p<n3/logn)个处理器上得到n3/p的并行处理时间;在不小于n3/logn个处理器上得到logn的并行处理时间。算法是由Dekel,Nassimi和Sahni三个人提出的,以他们名字的首字母命名。
先分析CREW PRAM体系结构上处理器个数p=n3的情况。由于矩阵相乘一共要进行n3次乘法运算,可以考虑给每个处理器分配一个乘法运算。分配办法是把a[i,
k]×b[k, j]分配给处理器 。然后每个处理器独立地进行乘法运算。下一步是把处理器 。然后每个处理器独立地进行乘法运算。下一步是把处理器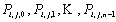 的内容加起来得到C[i,
j],这可以在logn时间内完成。由于是PRAM结构,无需考虑通信开销,因此算法完成需要一个单位时间的乘法运算和logn时间的加法运算,即算法的并行执行时间为logn。 的内容加起来得到C[i,
j],这可以在logn时间内完成。由于是PRAM结构,无需考虑通信开销,因此算法完成需要一个单位时间的乘法运算和logn时间的加法运算,即算法的并行执行时间为logn。
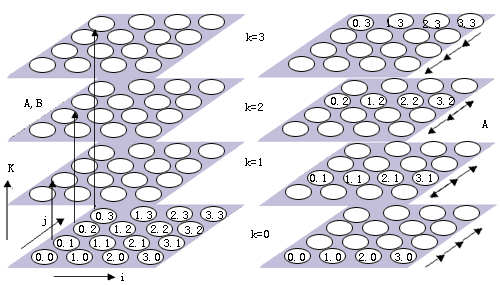
进一步,为了得到更实用的算法,我们把网络互联结构考虑进去,以超立方体为例展开讨论。设处理器个数P=n3=23d,为了说明问题,把处理器看成n个平面,每个平面上有n×n个处理器,参见图6.3.14。从图上可以看到,每个平面对应一个不同的k值。最初,对于参与乘积计算的两个矩阵A、B来说,每个矩阵都把自己的n2个元素分布在对应于k值为0的平面上,处理器Pi,j,0存储A[i,
j]和B[i, j]。
仍然象在CREW PRAM上那样,处理器Pi,j,*计算行A[I,
*]和列B[*, j]的点积。不同的是,在CREW PRAM上,由于每个处理器都可以通过访问共享内存而获得计算所需要的数据,而超立方体结构中则需要通过处理器之间的通信把计算所需要的数据传送到目标处理器,使得处理器Pi,j,k上存储有数据A[i,
k]和B[k, j]。
把数据放置到合适的处理器上可以通过两个通信步骤来实现。第一步把数据从k=0的平面复制到其它平面;第二步各个平面内部的数据扩散。第一步的数据复制机制可以用一句话来概括:把A[*,
j]复制到第k=j的平面;把B[i, *]复制到k=i的平面。第二步的数据扩散方式是:矩阵A的元素沿着j方向一对多通信复制;矩阵B的元素沿着i方向一对多通信复制。实例演示见图6.3.14。
经过这两个通信步骤后,A[i, k]和B[k, j]的乘积就可以在处理器Pi,j,k上进行了。处理器Pi,j,*上的乘积求和后在Pi,j,0上收集。
很容易知道,上述两步通信过程加一步乘法计算和求和结果需要的时间是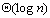 。因此,利用DNS并行算法在n3个处理器上需要 。因此,利用DNS并行算法在n3个处理器上需要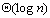 的时间。 的时间。
(a)
(b)
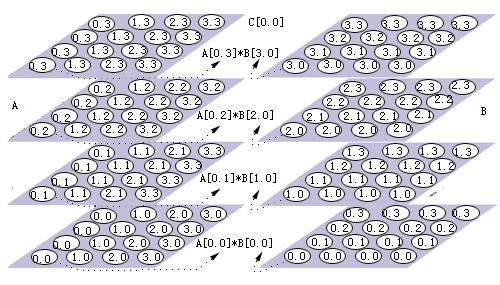
(c)
(d)
图6.3.14 DNS算法的演示(在64个处理器上完成两个4×4矩阵的相乘运算)
当处理器个数p<n3时,推理过程与上述相似。现在基于超立方体结构和切通路由(Cut-Through
Routing)来进行其时间性能分析。在前两步通信操作中,第一步对每个矩阵需要花费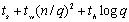 的时间;第二个通信步骤中每个矩阵需要花费 的时间;第二个通信步骤中每个矩阵需要花费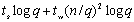 的时间;最后一步乘法计算需要(n/q)3的时间,而结果收集需要的通信时间是 的时间;最后一步乘法计算需要(n/q)3的时间,而结果收集需要的通信时间是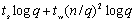 。上述时间求和,得DNS矩阵乘法的时间大约为: 。上述时间求和,得DNS矩阵乘法的时间大约为:
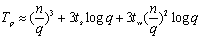
又因为q=p1/3,因此有:
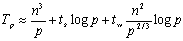
成本为:
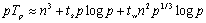
从上式可以知道,当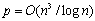 时, 时,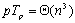 ,这说明当 ,这说明当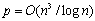 时,DNS算法能够在p(p<n3/logn)个处理器上得到n3/p的并行处理时间。 时,DNS算法能够在p(p<n3/logn)个处理器上得到n3/p的并行处理时间。
|