Cannon乘法的矩阵分块方式与简单分块矩阵法完全一样，但它没有等到所有的块A_ik与B_kj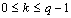（）都存储到本机后才进行C_ij的计算，而是每拿到一个A_ik和B_kj就进行乘法计算，小块计算完毕后就可以腾出空间给别的矩阵块使用。

　　算法的分为准备阶段和循环阶段，在准备阶段，块A_ij向左循环移动i步，B_ij向上循环移动j步。在循环阶段的每个循环中，处理器P_ij计算它上面两个当前块A_ij和B_ij的乘积，然后将A_ij向左循环移动一步，B_ij向上循环移动一步。所谓循环移动一步，就是移动一步之后取模，与算术移动相对应（可以联想到汇编语言中的循环移位）。

　　图6.3.12演示了在16个处理器上完成两个4×4矩阵A和B相乘的过程。在准备阶段，矩阵A的第0行（A₀₀到A₀₃）不动，即向左移动0步；A₁₀至A₁₃向左循环移动一位；A₂₀至A₂₃向左循环移动2位；A₃₀至A₃₃向左循环移动3位。矩阵B的第0列（B₀₀到B₃₀）向上移动0位；B₀₁至B₃₁向上循环移动一位；B₀₂至B₃₂向上循环移动2位；B₀₃至B₃₃向上循环移动3位。在循环阶段，每计算一次块矩阵的乘法就把用过的块矩阵A移动给左邻居，把块矩阵B移动给上邻居。
　　
　　Cannon算法的性能分析可以参照简单分块矩阵法给出，在此省略。