|
利用分块矩阵操作的串行矩阵相乘算法
图6.3.11的算法很容易并行化,这里讨论两个参与相乘的矩阵均采用块棋盘划分的情况。设参与计算的矩阵为A=(aij),B=(bij),计算结果矩阵为C=(cij),处理器个数p=q2。把两个矩阵均分成p个子块Aij和Bij,每个子块的大小为(n/q)×(n/q);将这些子块分配到q×q个处理器上。为了计算块Cij,需要所有的块Aik与Bkj(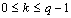 ),为此需要多个处理器之间的通信操作。矩阵分块后,整个算法过程分为两步:通信、计算。通信过程得到计算所需要的矩阵块;计算过程根据源矩阵块经过乘法和加法运算得到目标矩阵块。 ),为此需要多个处理器之间的通信操作。矩阵分块后,整个算法过程分为两步:通信、计算。通信过程得到计算所需要的矩阵块;计算过程根据源矩阵块经过乘法和加法运算得到目标矩阵块。
第二步计算是在单个处理器上完成的,与网络互联结构没有关系,所需要的时间量级为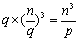 。通信时间虽网络互联结构的不同而不同。在二维网格结构和超立方体结构中的通信时间分别为: 。通信时间虽网络互联结构的不同而不同。在二维网格结构和超立方体结构中的通信时间分别为:
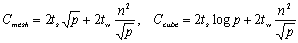
所以算法总的运行时间为:
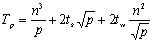 (二维网格) (二维网格)
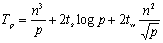 (超立方体) (超立方体)
除了运行时间外,再以超立方体互联结构为例来考察一下此并行算法的其它性能指标:加速比、效率、成本。
加速比定义为最好的串行算法与此并行算法运行时间的比值,姑且把O(n3)看作串行矩阵相乘的最优时间复杂度,则算法的加速比为:
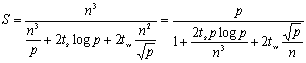
算法的效率为:
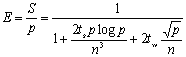
算法的成本为:
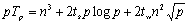
可以看到,当p远小于n时,算法的加速比为近似为p,效率接近1。当p<n2时,并行算法与串行算法的成本处于同一量级。但是并行算法在执行过程中需要占用较多的存储空间(每个处理器需要容纳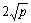 个大小为n2/p的块共占用 个大小为n2/p的块共占用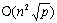 的存储空间),需要开发新的并行算法以节省存储空间。 的存储空间),需要开发新的并行算法以节省存储空间。
|