矩阵乘法的计算公式是：
　　　　　　　　　　　
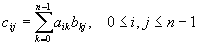
　　其中。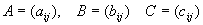

　　最简单直观的矩阵乘法的串行算法见图6.3.10。此算法每计算结果矩阵的一个元素需要n的时间，n²个元素所需要的总时间为n³。O(n³)不是矩阵乘法的最低时间复杂度，通过搜索引擎以"Fast Matrix Multiplication"为关键词可以查找到很多由于快速矩阵乘法运算的网页和论文。现在已经证明，矩阵相乘的串行算法复杂度不可能小于O(n²)。最著名的快速算法是由Strassen提出的，算法把矩阵相乘分解为若干子矩阵乘积的和，然后逐次递归分解下去。目前已知最低的时间复杂度为O(n^2.376)，由Coppersmith和Winograd在1990年提出。为了简单起见，本小节的并行化仍然基于图6.3.10所描述的传统算法。
　　　　　　
　　　　　　　　　　　　　矩阵相乘的串行算法

　　在开始并行化之前，先引入分块矩阵操作的概念。在进行矩阵操作时，我们总是倾向于把矩阵操作转化为对矩阵元素的操作。其实，可以把一个子矩阵块看作一个超元素，把矩阵操作转化为对矩阵块（超元素）的操作；如果有必要，矩阵块还可以进一步分解为更小的矩阵块。这种概念叫做分块矩阵操作。比如一个n×n的矩阵可以看作由q×q个矩阵块所构成，每个矩阵块是一个(n/q)×(n/q)的矩阵。