|
超立方体互联结构上的矩阵转置
转置也可以递归地进行,称为递归转置算法(Recursive Transposition Algorithm)。基本思路是一个n×n的矩阵先分成4个子矩阵,把每个子矩阵看作一个整体对整个大矩阵进行转置;然后每个子矩阵再分成4个更小的矩阵,逐次递归,参见图6.3.5。
8×8矩阵的递归转置
这种递归跟超立方体的递归构建过程很像。利用这一点可以在超立方体上实现矩阵转置。如图6.3.6所示,先把n×n的矩阵分成4个(n/2)×(n/2)的子矩阵,相应地,一个具有p个处理器的超立方体可以看作是4个p/4超立方体所构成。递归一直到每个子超立方体只含有一个处理器为止。来分析算法的运行时间,经过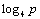 次后递归结束,此时各个子块的大小为 次后递归结束,此时各个子块的大小为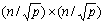 ,这些子块内部转置的时间量级为n2/p。每个待通信的子块大小为n2/p,使用存储转发选路所需的时间为2( ,这些子块内部转置的时间量级为n2/p。每个待通信的子块大小为n2/p,使用存储转发选路所需的时间为2(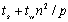 ),递归 ),递归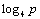 次的总通信时间为 次的总通信时间为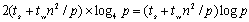 。这样,算法总的运行时间为: 。这样,算法总的运行时间为:
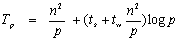
16个处理器的超立方体上所进行的并行矩阵递归转置
|