|
一个d维的超立方体可以看作是由两个d-1维的超立方体互联而成的,利用这一点,可以把一个d维的超立方体中存储的一个序列划分成两个子序列而分别存放到两个d-1维的超立方体上,使得每个d-1维立方体的每个处理器都跟另外一个立方体的某处理器直接相连。这样,根据一个大于界的子序列与小于界的子序列可以分别放在不同的超立方体上。
设处理器个数p=2d构成一个d维的超立方体,处理器按照从0到2d进行二进制编码;n个元素所构成的序列均匀分布到各个处理器上,使得每个处理器上有n/p个元素。现在选择一个界元素,并将它的值广播到各个处理器,各个处理器中最高位编码值为1的处理器与最高位编码值为0的处理器之间进行元素的部分交换,使得最高位编码值为1的处理器上的所有元素均大于界值,最高位编码值为0的处理器上的所有元素均小于或等于界值。这样就把维数为d的超立方体划分成了两个独立的维数为d-1的超立方体。对每个维数为d-1的超立方体重复上面的操作,参见图6.2.8。
从上面的算法描述可以看出,界的选择对于算法的性能有着直接的影响。界把序列分割得越均匀,则算法性能越好。一个相对比较好的界选择方式是处理器在自己拥有的所有元素中值元素作为界值。按照这种界选择策略,算法每次迭代可以分四步:局部排序;界选择;界值广播;元素交换。局部排序的时间复杂度为 ;排序排序后再选择界的时间复杂度为 ;排序排序后再选择界的时间复杂度为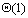 ;第i次迭代需要消耗的通信时间是 ;第i次迭代需要消耗的通信时间是 ,d次迭代共消耗 ,d次迭代共消耗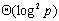 的时间;由于交换只可能发生在相邻的处理器之间,每次迭代的时间最多为 的时间;由于交换只可能发生在相邻的处理器之间,每次迭代的时间最多为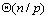 ,d次迭代共花费 ,d次迭代共花费 。因此总的并行处理时间为: 。因此总的并行处理时间为:
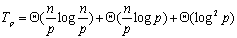
由于串行处理时间为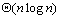 ,因此算法的加速比S与效率E分别为: ,因此算法的加速比S与效率E分别为:
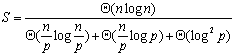
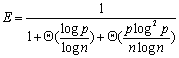
|