|
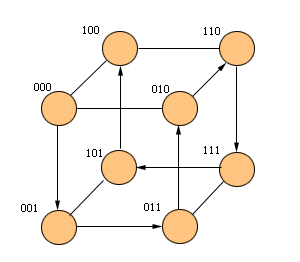
图6.2.7 用格雷码把一个链映射到超立方体上(带箭头的粗实线表示链)
设有n个元素待排序,p=2d 个处理器构成一个超立方体结构,则每个处理器上分布有n/p个元素。处理器之间虚拟为一个链状结构并沿着链从0到2d-1进行编号,然后根据格雷码(Gray-code)把处理器映射到一个超立方体上,见图6.2.7。算法分三个阶段:本地操作、远程交换、奇偶置换冒泡。
第一阶段,各个处理器对本地的n/p个元素进行排序操作,复杂度为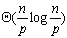 。 。
第二个阶段分d个步骤。第1个步骤虚拟链上编号为0的处理器与编号为2d-1的处理器之间进行元素比较和交换操作,编号为1与2d-1的处理器之间进行元素比较和交换,……。总之是编号之和为2d-1的处理器之间两两进行元素比较和交换。第2个步骤把虚拟连拆成两个长度相等的子链,第一条链编号从0到2d-1-1,第二条链编号从2d-1到2d-1。然后对这两条链分别进行类似第一步的操作。第3个步骤在把步骤2的两条子链等拆分共形成4条链,每条子链进行步骤1的元素比较和交换操作。每一步骤需要花费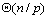 的时间, 的时间,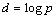 步的时间花费为 步的时间花费为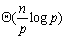 。 。
第三个阶段按照上一小节所述的奇偶置换冒泡排序相类似的步骤,所不同的是当处理器之间没有元素交换时则终止循环。因为第一步操作使得距离自己本来的位置较远的元素移动到了较近的位置,所以第二步奇偶置换操作的循环次数将大大减少。设循环次数为r,则本阶段的复杂度为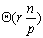 。 。
把三个阶段的时间相加,得到整个算法的并行处理时间:
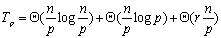
在n和p为定值的情况下,算法的效率决定于r。如果r很小,则本算法优于奇偶置换算法。如果r与p为同一量级,则本算法与奇偶置换算法的性能类似。
|