经常会关心的一个问题是如果处理器的数量不受限制的话，一个应用问题多长时间能够算完，或者，一个并行算法的最小可能运行时间是多少。当对一个特定的问题规模增加处理器数目的时候，要么并行运行时间持续减少，直到它渐进于一个最小值，要么在达到一个最小值后它又开始增加（思考：为什么？）。对一个给定的工作负载W，可以确定最小并行运行时间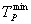（求出T_p对p的驻点，这里假设T_p(W,p)对p可微），取最小值时的p值可以由下面的方程决定：
　　　　　　　　　　　　　
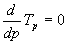
　　令p₀是满足上面方程的一个解，用它代入T_p的表达式，就可以得到。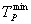

　　一个例子
　　在p个处理器的超立方体上完成n个数的加法（p < n，其中p和n都是2的整数次幂），求最小执行时间。

　　前面已经讨论过，并行运行时间可以用下面的公式近似的表示：
　　　　　　　　　　　　　
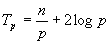
　　式子两边对p进行微分，并令它为0，则有：
　　　　　　　　　　　　　
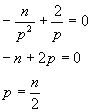
　　将这个值代入上面的表达式，就可以得出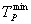
　　　　　　　　　　　　　
　　上面的例子中，当p=p₀时处理器-时间积为，这比问题的串行算法的复杂度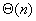要高，因此，能够得到最小并行运行时间的并行系统并不是开销最优的。