|
一个例子
并发度对等效率函数的影响。
考虑用高斯消元法解一个n变量n个方程的线性方程组。总的计算量为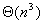 ,但n个变量必须依次消除,而消除一个变量需要的计算量为 ,但n个变量必须依次消除,而消除一个变量需要的计算量为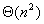 ,因此,在算法运行的任意时刻,最多有 ,因此,在算法运行的任意时刻,最多有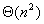 个处理器能够保持工作状态。由于问题规模为 个处理器能够保持工作状态。由于问题规模为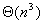 ,所以算法的并发度 ,所以算法的并发度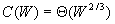 。这说明最多有 。这说明最多有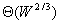 个处理器能够被有效的使用。另一方面,给定p个处理器,问题规模至少应该为 个处理器能够被有效的使用。另一方面,给定p个处理器,问题规模至少应该为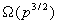 才能有效的利用所有的处理器,因此,由于并行度的限制,这个并行系统的等效率函数为 才能有效的利用所有的处理器,因此,由于并行度的限制,这个并行系统的等效率函数为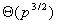 。 。
由并行度限制的等效率函数最优(也即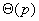 )的必要条件是并行算法的并发度为 )的必要条件是并行算法的并发度为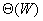 ,如果一个算法的并发度比 ,如果一个算法的并发度比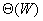 要低,那么并行度限制的等效率函数比 要低,那么并行度限制的等效率函数比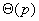 要高,这种情形下,一个并行系统的总的等效率函数由并行度限制的等效率函数,通信限制的等效率函数,和其他额外开销限制的等效率函数中的最大值确定。 要高,这种情形下,一个并行系统的总的等效率函数由并行度限制的等效率函数,通信限制的等效率函数,和其他额外开销限制的等效率函数中的最大值确定。
等效率度量指标的最大优点是,可以用简单的、可定量计算的、少量的参数就能计算出等效率函数,并由其复杂度就可以指明算法的可扩展性。这对于具有网络互连结构的并行计算机来说是很合适的,因为To是可以一步一步计算出来的。而且To是计算等效率函数的唯一关键参数,所以如果它不能够方便的计算出来,则用等效率函数度量可扩展性的方法就受到了限制。我们知道开销To通常包括了通信、同步、等待等额外计算开销。不幸的是,在共享存储的并行计算机中,To则主要是非局部访问的读/写时间、进程调度时间、存储竞争时间以及Cache一致性维护时间,而这些时间是难以准确计算的,所以用解析计算的方法不应该是一种唯一的方法。1994年两位中国学者Xian-He
Sun和Xiao-Dong Zhang分别提出了以实验测试为主要手段的两种衡量可扩展性的指标,即等速度(isospeed)和平均延迟指标。
|