|
前面给出了开销最优的定义,这里再强调一次:如果一个并行系统的处理器-时间积与单处理器上的已知最快得串行算法的执行时间成比例,那么这个并行系统就是一个开销最优的并行系统,用公式表示为
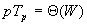
将左边的处理器-时间积用问题规模和额外开销的函数表示,可以得到下面的公式
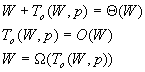
上面的公式说明,一个并行系统是开销最优的充分必要条件是它的额外开销函数不渐近的超过问题规模。这个条件与增加处理器数目而保持等效率的条件是非常相似的。如果等效率函数为f(p),那么当一个并行系统扩大规模时,为了保证系统开销最优,必须要满足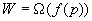 。下面的例子说明了开销最优与等效率函数的关系。 。下面的例子说明了开销最优与等效率函数的关系。
一个例子
开销最优与等效率函数的关系。
考虑p处理器的超立方体上n个数的加法,一个非开销最优的并行系统的并行算法有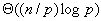 的时间用于通信,它的额外开销函数是 的时间用于通信,它的额外开销函数是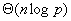 ,n个数的加法的问题规模为 ,n个数的加法的问题规模为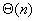 ,这个并行系统的等效率函数并不存在,因为不存在常数K(也就是E)使得等效率公式成立,额外开销总是要大于问题规模,因此,这个系统是不可扩展的并行系统。 ,这个并行系统的等效率函数并不存在,因为不存在常数K(也就是E)使得等效率公式成立,额外开销总是要大于问题规模,因此,这个系统是不可扩展的并行系统。
下面考虑这个问题的开销最优的并行系统,对这个并行系统,有
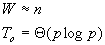
这样,它的等效率函数为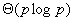 ,而前面的例子中已经得出结论,这个并行系统开销最优的条件是 ,而前面的例子中已经得出结论,这个并行系统开销最优的条件是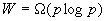 ,可以很清楚地看到它们之间的等价性。 ,可以很清楚地看到它们之间的等价性。
|