并行运行时间可以被表示成问题规模、额外开销函数和处理器数目的函数，重写上面的公式，可以得到并行运行时间的表达是：
　　　　　　　
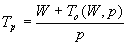
　　则加速比可以表示成：
　　　　　　　
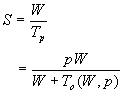
　　而效率可以表示成
　　　 　　　
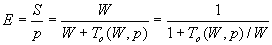
　　根据这个效率函数，如果问题规模保持不变，当p增加时，效率会降低，因为总的额外开销会随着p的增加而增加。如果处理器数目保持不变，增大问题规模，那么对可扩展的并行系统，效率会提高，这是因为对固定的处理器数目p，额外开销函数的增长速度要比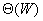慢，对这些并行系统，增加p时，可以通过增大W的方法来得到需要的系统效率。

　　对不同的并行系统，为了得到稳定的效率，当处理器数目增加时，W必须以不同的速率相应增加，比如，在某些情形下，当处理器数目增长时，为了保持效率不变，W需要以p的指数函数的速率增长。这样的系统的可扩展性很差，因为当使用大量的处理器时，并行系统很难得到良好的加速比，除非采用巨大的问题规模。另一方面，如果相对p的增长，为了保持效率不变，问题规模只需要以p的线性函数形式增长，那么这样的系统具有较高的可扩展性，这是因为当处理器的数目增加后，只需要采用合理的问题规模就可以得到较好的加速比。

　　对可扩展的并行系统，效率可以维持在一个固定的值，只要T_o/W保持不变。设E为所需要的并行系统效率，根据前面的效率表达时，有
　　　　　　　
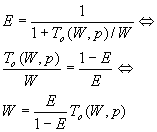
　　令K=E/(1-E)，当给定效率后，这是一个常数。因为T_o是W和p的函数，则上面的表达式可以写成
　　　　　　　
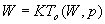
　　这样，可以通过代数变换的形式，将W表示成p的函数，这个函数描述了为了保持效率不变，当p改变时所需要的问题规模，我们把这个函数称为一个并行系统的等效率函数，这个等效率函数确定了一个并行系统为了保持效率为常数，从而使加速比随处理器数目成比例的增长的容易程度，它描述了并行系统的可扩展能力。一个小的等效率函数意味着当处理器数目增长时，只需要较小的问题规模增长就可以达到处理器的充分利用，对应的并行系统当然具有很高的可扩展能力。相反的，一个大的等效率函数对应着一个可扩展性很差的并行系统。
　　
　　对不可扩展的系统来说，等效率函数不存在，因为对这种并行系统，当处理器数目增加时，不管如何增加问题规模，都不可能使系统的效率保持为常数。