|
在分析并行系统的时候,经常会碰到的一个概念是问题的规模。前面实际上已经多次非正式的用到了问题规模这个术语,这里给出对它的准确定义。一个直接的方法是将问题规模定义为一个描述输入规模的参数,比如在矩阵乘法中,如果矩阵为n×n,那么问题规模就是n。这种定义方法的缺点是当面对不同的问题时,对问题规模需要作不同的解释。比如,将输入规模加倍,矩阵乘法的运行时间变为原来的八倍(假定采用的矩阵乘法的时间复杂度为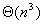 ,而不考虑复杂度更低的算法),而矩阵加法的运行时间变为原来的四倍。 ,而不考虑复杂度更低的算法),而矩阵加法的运行时间变为原来的四倍。
一个一致性的定义应该是,对所有的问题,问题规模加倍意味着需要执行的运算也变为原来的两倍。因此,我们选择解决问题所需要的基本操作的总数量来作为问题规模的定义。采用这个定义,n×n的矩阵乘法的问题规模就是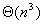 ,而n×n的矩阵加法的问题规模是 ,而n×n的矩阵加法的问题规模是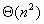 。为了使问题规模的定义对给定的问题唯一,我们定义一个问题的问题规模为在单处理器上解决这个问题的最优串行算法的基本计算步骤的数目。这里所说的最优串行算法指的是已知的性能最好的串行算法。 。为了使问题规模的定义对给定的问题唯一,我们定义一个问题的问题规模为在单处理器上解决这个问题的最优串行算法的基本计算步骤的数目。这里所说的最优串行算法指的是已知的性能最好的串行算法。
由于问题规模定义为串行时间复杂度,所以它是输入大小的函数,用符号W来表示一个问题的问题规模。下面的讨论中,都假设算法的每个基本计算步骤可以用单位时间完成。这个假设不会影响对并行系统的任何分析:因为其他的与硬件相关的常数,比如消息传递启动时间,每个字的传输时间和每一跳(hop)的时间,都可以用基本计算步骤的时间来进行标准化。在这个假设条件下,问题规模W等于在一个串行计算机上解决这个问题的最快的已知算法的串行运行时间Ts。
|