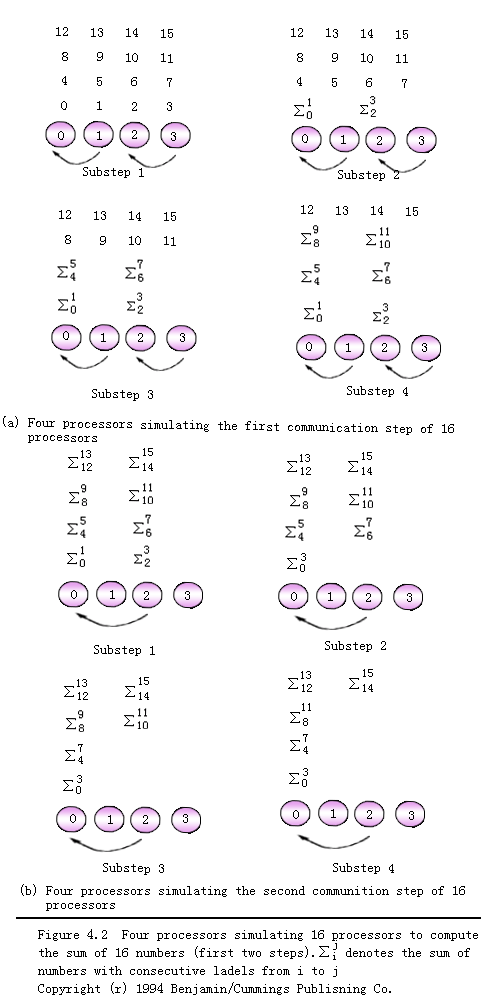在n个处理器的超立方体结构的并行计算机上完成n个数据累加不是一个开销最优的并行系统，这个并行算法中假定处理器的数目与数据的数目是一致的。但在实际中，由于处理器数目是固定的，而输入数据的数目则是可变得，因此每个处理器上往往会分配很多的数据，这相当于增加每个处理器的计算粒度。用比系统中最大可能处理器数要少的处理器数来运行并行算法称为并行系统的处理器降规模（Scaling down）。一个降规模的方法是，设计一个并行算法使得每个处理器上一个数据，然后用少量的处理器来对大量的处理器进行仿真。如果有n个输入数据，而仅仅有p个处理器（p < n），我们可以使用为n个处理器设计的并行算法，此时在程序员眼中，这实际上是n个虚拟处理器，在运行时，用p个物理处理器来进行仿真，每个处理器需要模拟n/p个虚拟处理器。

　　当处理器数目下降n/p倍，每个处理器上的计算量增加了n/p倍，因为现在每个处理器实际上需要完n/p个处理器的工作。如果虚拟处理器被恰当的映射到物理处理器上，总的通信时间不超过原来的n/p倍（为什么？）因此，总的并行运行时间最多是原来的n/p倍，而处理器-时间积不会增加。因此，如果一个p处理器的并行系统是开销最优的，用p个处理器来对n个处理器（p < n）进行仿真保持系统的开销最优。

　　这种增加计算粒度的方法的缺点是，如果一个并行系统本身不是开销最优的，那么计算开销增加后，它可能仍然不是开销最优的。我们用下面的例子来说明这个问题。

　　一个例子
　　在p个处理器的超立方体上完成n个数的加法（p < n，其中p和n都是2的整数次幂）。
　　我们采用前面的面向n个处理器的算法，然后用p个处理器来对n个处理器进行仿真。下面的图描述了n=16和p=4时的解题过程。