在实际应用中，可供参考的加速比经验公式为：
　　　　　
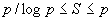
　　可以达到线性加速比的应用问题有矩阵相加、内积运算等等，这一类问题几乎没有通信开销，而且单独的计算之间几乎没有什么关系；对于分治类的应用问题，它类似于二叉树，处于树上的同级节点上的计算可并行执行，但越靠近根，并行度将逐渐减少，此类问题可能可以达到p/logp的加速比；对于通信密集型的应用问题，它的加速比经验公式可以参考下面的式子：
　　　　　S=1/C(p)

　　其中，C(p)是p个处理器的某一通信函数，或者为线性的或者为对数的。

　　严格的线性加速比对大多数应用问题来说，是难以达到的，更不用说超线性加速比。但在某些算法或者程序中，可能会出现超线性加速比现象，比如，在某些并行搜索算法中，允许不同的处理器在不同的分支方向上同时搜索，当某一处理器一旦迅速的找到了解，它就向其余的处理器发出中止搜索的信号，这就会提前取消那些在串行算法中所做的无谓的搜索分枝，从而出现超线性加速比现象；在大多数的并行计算系统中，每个处理器都有少量的高速缓存，当某一问题执行在大量的处理器上，而所需要的数据都放在高速缓存中时，由于数据的复用，总的计算时间趋于减少，如果由于这种高速缓存效应补偿了由于通信造成的额外开销，就有可能造成超线性加速比。
最后值得指出的是，加速比的含义对科学研究者和工程实用者可能有所不同。对一个给定的问题，可能会有不止一个的串行算法，它们的运行时间也不会完全相同，这就带来了不同的加速比的定义。

　　研究者们使用绝对加速比的定义，即对于给定的问题，加速比等于最佳串行算法所用的时间除以同一问题的并行算法所用的时间。（思考：如何得到最佳串行算法？）对最佳串行算法有几个说明。因为最佳串行算法也是通过实际运行测出来的，按照串行算法运行平台的不同，绝对加速比也可以分成两种。一种与具体的机器有关，即串行计算机采用与并行计算机一样的处理器；一种与具体的机器无关，此时的串行算法运行时间是串行计算机上的最短执行时间。但有的时候，对一个特定的问题，它的最佳串行算法是未知的，或者，它的串行算法所需要的运行时间太长，实际运行它是不太现实的，在这些情况下，经常用已知的最优串行算法来代替最佳串行算法；

　　而工程中使用相对加速比的定义，即对于给定的问题，加速比等于同一个算法在单处理器上运行的时间除以在多处理器上的运行时间。显然，相对加速比的定义是比较宽松和实际的。

　　一个例子
　　在n个处理器的超立方体上完成n个数的加法：开始时，每个处理器都存放了一个待加的数据，算法结束时，其中的一个处理器中已经存放了n个数累加的结果。

　　假定n=2^m，m是正整数，我们可以在一个超立方体或者共享存储多处理器系统上用m=logn个步骤完成这个算法，下面的图描述了n=16时的算法执行情况，处理器从0到15依次编号，相邻处理器（从i到j）中数据的部分和用∑_i^j表示。