给定一个存储受限问题，假定在单节点上使用了全部存储容量M并在相应于W的计算时间内求解，此时工作负载W=fW+(1-f)W。在p个节点的并行系统上，能够求解较大规模的问题是因为存储容量可以增加到pM。用因子G(p)来反映存储容量增加p倍时工作负载的增加量，所以增加后的工作负载W=fW+(1-f)G(p)W。那么，存储受限的加速比公式为：

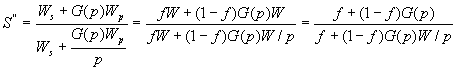
　　Sun和Ni定律的几何意义可以清楚的用下面的图来表示：

　　如果考虑到并行程序运行时的额外开销W_o，则上面的公式应该作相应的修改：
　　

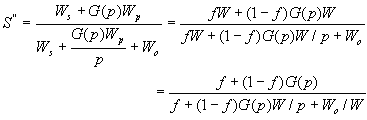
　　当G(p)=1时，它变为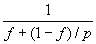 ，这就是Amdahl定律，当G(p)=p时，它变为f+p(1-f)，这就是Gustafson定律，当G(p)>p时，它相应于计算负载比存储要求增加得快，此时Sun和Ni定律指出的加速比比Amdahl和Gustafson定律指出的都要高。