Gustafson定律的基本出发点是：

　　(1) 对于很多大型计算，精度要求很高，即在此类应用中精度是一个关键因素，而计算时间是固定不变的。此时为了提高精度，必须加大计算量，相应的也必须增加处理器的数目来完成这部分计算，以保持计算时间不变；

　　(2) 除非学术研究，在实际应用中没有必要固定工作负载而使计算程序运行在不同数目的处理器上，增多处理器必须相应的增大问题规模才有实际的意义。因此研究在给定的时间内用不同数目的处理器能够完成多大的计算量是并行计算中一个很实际的问题。

　　(3) 对大多数问题，问题规模的改变只会改变计算中并行计算量，而不会改变串行计算量。

　　从这些动机出发，Gustafson在1987年提出了变问题规模的加速比模型：

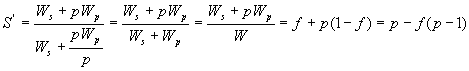
　　当p充分大时，S'与p几乎成线性关系，其斜率为1-f，这就是Gustafson加速比定律，它意味着随着处理器数目的增加，加速比几乎与处理器数目成比例的线性增加，串行比例f不再是程序的瓶颈，这为并行计算系统的发展带来了非常乐观的结论。

　　Gustafson定律的几何意义可以清楚的用下面的图来表示：

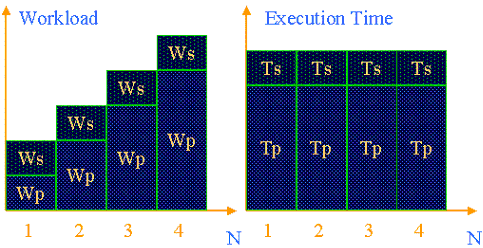
　　当处理器数目n=1024，加速比Sn随α变化的情况如下：可以用图表示如下：
　　　　



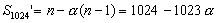
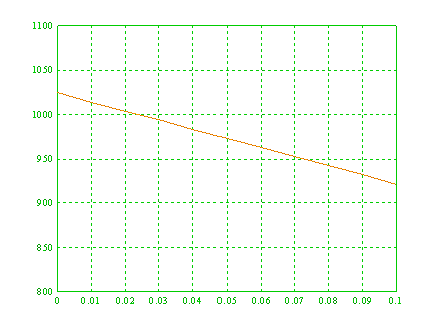
　　同样的，当考虑到并行程序运行时的额外开销时，Gustafson定律应该修改为：
　　　

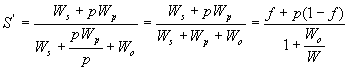
　　注意：W_o是p的函数，它可能会随着p的改变而改变。要到达一般化的Gustafson定律所描述的线性加速比，当p改变时，必须要控制额外开销的增长，这在实际中往往是非常困难的。