Amdahl定律的基本出发点是：

　　(1) 对于许多科学计算，实时性要求很高，即在这类应用中计算时间是个关键性因素，而计算负载是固定不变的。为此，在一定的计算负载下，为满足实时性的要求，可以通过增加处理器数目的方法来减少运行时间，提高计算速度；

　　(2) 因为固定的计算负载可以分布在多个处理器上，这样增加了处理器就加快了执行速度，从而达到了加速的目的。

　　在这样的动机推动下，1967年Amdahl推导出了固定负载情况下的加速比公式：
　　　　　　
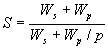
　　由于W=Ws + Wp，上式右边分子分母同除以W，则有
　　　　　　
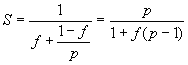
　　当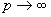 时，加速比的极限为
　　　　　　

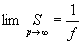
　　这就是著名的Amdahl加速定律，它意味着随着处理器数目的无限增大，并行系统所能达到的加速比存在上限，且为一个常数1/f，这个常数只取决于应用本身的性质。这个结论在历史上曾经对并行系统的发展带来了一种悲观的影响。它带来的两种影响是，一是劝阻并行计算机厂商生产更大规模的并行计算机，二是促进了并行编译计算的发展，以降低程序中串行部分的值。

　　Amdahl定律的几何意义可以清楚的用下面的图来表示：

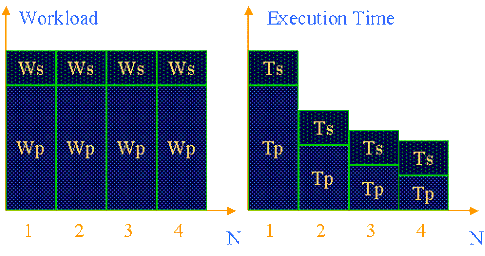
　　当处理器数目n=1024，加速比公式如下，Sn随α变化的情况如下图：
　　　
　　

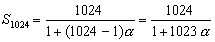
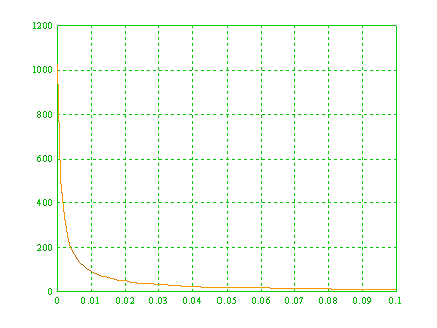
　　实际上并行加速比不仅受限于程序的串行分量的比例，而且也受并行程序运行时的额外开销的影响。如果考虑到这部分因素的影响，令W_o为额外开销，那么上面的公式应该修改为：
　　
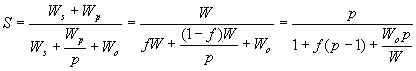
　　这种情形下的加速比极限为：
　　　　　

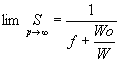
　　结论：并行程序中的串行分量比例和并行额外开销越大，则加速比越小。