H-PRAM模型的构成
　　1992年，T. Heywood等人在PRAM的基础上，提出了分层结构的PRAM模型，即H-PRAM模型：

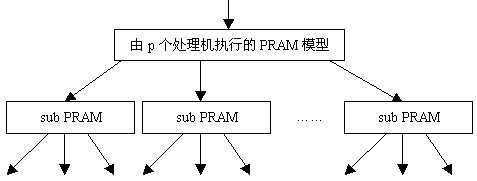
　　H-PRAM模型以PRAM为子模型，在第一层(算法入口处)中，由p个处理机执行的PRAM算法除了执行PRAM指令外，还要执行分割指令。它将p个处理机分成多个不相交的子集，每个子集分配一个同步PRAM算法（对应于第二层中的Sub PRAM算法），每个Sub PRAM算法内部是同步的，它们之间是异步的。第二层的Sub PRAM算法在执行分割指令，一直下去，直到最后一层中的Sub PRAM 算法只由一台处理机执行时为止。每个Sub PRAM算法执行完后，等待其它Sub PRAM算法完成。

　　通常在每个分割指令后由一个同步操作（称为β同步），当β同步完成后，上一层的PRAM或Sub PRAM开始执行下一条指令。分割指令的时间复杂性等于在每个Sub PRAM上运行PRAM算法所需时间的最大值。当估算第n层每个Sub PRAM算法复杂性时，n+1层上所有Sub PRAM算法复杂性估算都已完成，为已知信息。所以，整个算法的时间复杂性估计从层次结构的最底层开始。

　　H-PRAM模型的两种变型
　　（1）私有的H-PRAM模型。共享存储器处理机成比例分割，其延迟为Sub PRAM规模的函数。
　　（2）共享的H-PRAM模型。共享存储器不分割，其延迟对所有Sub PRAM模型都是相同的。

　　Sub PRAM算法的复杂性
　　H-PRAM模型将算法中最大连续的多个计算操作定义为一个计算段，计算段之前是算法入口或通信操作，计算段之后是通信操作或算法出口，每个通信段后进行同步（称α同步）。假设第n层的某个Sub PRAM算法中有T个计算操作、C个通信操作、t个计算段、Q个分割操作，延迟为L， α同步开销为A，Q个分割操作和Q个β同步开销为R，由于PRAM算法每个操作所花时间为单位时间，所以该Sub PRAM 算法的时间复杂性为：
　　　　　　　T+t*A+C*L+A

　　H-PRAM模型的特点
　　(1)具有PRAM模型的简单性。
　　(2)在PRAM模型的基础上加入了异步层次控制，且不要求在系统中加入同步原语。包括：
　　● 控制的异步 第n层的Sub PRAM内部是同步的，但它们之间是异步的。
　　● 通信的异步 在私有的H-PRAM模型中，各个Sub PRAM所对应的主存是不同的，一般不允许异步通信。假如有某个Sub PRAM想访问另一个Sub PRAM的共享主存单元，必须在拥有该主存单元的Sub PRAM先访问该单元，并且与其处于同一层的所有Sub PRAM均完成任务时，进行β同步进入下一层后，这个Sub PRAM才可进行这个访问操作。这样可保证程序的确定性。
　　● 在共享H-PRAM中，允许异步通信，但要求在编程模型中，在不同的Sub PRAM的两个处理机对同一主存单元进行的两次访问之间加入β个同步，这样可避免非确定性。
　　（3）对通信和同步提供了抽象控制。在私有的H-PRAM中，将所有处理器分割成更小的子集，处于同一子集中的处理机之间可进行通信和同步。这反映了本地性，促进了网络拓扑的最优化。
　　（4）模型中加入了延迟参数。
　　（5）系统增大时，通信带宽要比计算带宽增加得快，此能保持效率。
　　（6）反映了流水线的预取技术。

　　当处理机访问某个字时，相邻的g个字可在L+O(g)时间内取出，同时反映了不相邻的g个字可在L+O(g)时间内取出。

　　H-PRAM模型的不足
　　由于H-PRAM模型使用PRAM模型作为子模型，因此不足表现在：
　　（1）当系统中各处理机速度相差较大时，需要进行层次分割后才能直接支持H-PRAM模型。
　　（2）认为延迟L只是处理机个数的函数，而未考虑引起延迟的其它因素（如网络拥挤、重发机制等）。
　　（3）对通信两端的准备发送和准备接收的开销未加考虑。
　　（4）对多线程的上下文切换的开销未加考虑。