增加粒度

　　在划分阶段，为了尽可能地开发问题的并行性，可能产生了大量的细粒度任务。但是大量的任务可能会增加通信开销和任务创建开销。

　　表面-容积效应（Surface-to-Volume Effects） 通常，一个任务的通信需求正比与它所操作的数据域的表面积，而计算需求正比于它所操作的数据域的容积。因此一个计算单元的通信与计算之比随任务尺寸的增加而减小。例如在二维问题中，"表面积"即是数据域的周长，它正比于问题的尺寸，而"容积"指数据域的面积，它正比于问题尺寸的平方。

　　以二维平面上的雅可比有限差分法5点格式为例。假设需要计算的数据是4×4矩阵。如果把计算每个元素算作一个任务，则有16个任务。每轮迭代中，每个任务都需要与其上下左右的任务通信，共需48次通信（当然这些通信中许多可以并行进行）。如下图（a）所示，每个箭头表示一次通信。
　　

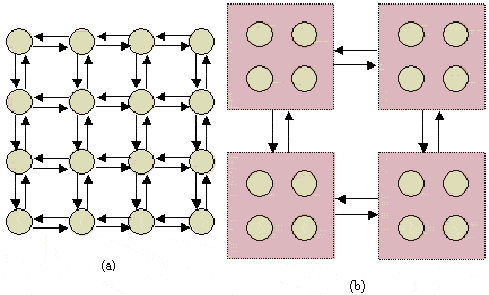
　　如果将相邻的四个元素的计算作为一个任务则只需8次通信，如上图（b）所示。虽然每次通信要传递两个数据，但是相对于图（a），通信的次数和通信量都大大减少了。可见，当小任务组合为大任务后，原来的某些数据传递被"包含"在大任务里面了，它们不再表现为通信，实际计算时，这些数据交换可以通过直接读取内存完成。这正是增加粒度可以减少通信的原因。

　　上例我们只想说明增加粒度可以减少通信次数和通信量。仔细思考我们会发现在上例中，图（b）的通信开销可能比图（a）大。设通信建立的时间为S，传递一个数据的时间为t。假设图（a）的通信方式是方向相同的所有通信同时执行。比如所有的任务同时先向左传递，那么所有向左的通信需时间S+t。同理，向其它三个方向的通信各需时间S+t。所以图（a）的通信开销是4(S+2t)。对图（b）也可进行相同的分析，但是图（b）中每个通信要传递两个数据，因此总的通信开销是 ，比图（a）大。

　　上例中的通信是均匀的，且可以并行执行。实际上，实际问题的各小任务之间的通信很可能是不均匀的。比如一个问题可以分为A，B C三个任务，A与B之间通信频繁，而它们与C之间通信很少。那么显然应该将 和 组合成一个大任务，以避免通信对它们并行执行造成的影响。但是组合之后，出现了一个较大的任务，完成这个大任务可能需要更长的时间。这时就需要权衡，看哪种方案更好。