欲使用借用法时，要注意观察问题的特征和算法的结构、形式，联想与本问题相似的已有算法。可以注意寻找要解决的问题与某些著名问题之间的相似性或本问题的算法与某些著名算法之间的相似性。同时，借来的方法使用起来效率要高。成功地"借用"不是件容易的事。

　　下面介绍求解图中任意两结点间最短路的并行算法。它是通过借用矩阵乘法算法设计的。

　　设在一有向图中，各弧都赋予了非负整数权。图中一条路径的长度定义为该路径上所有的弧的权的和。图中两结点之间的最短路径是指它们之间长度最短的路径。

　　设G为一个含有n个结点的有向图。矩阵W=(w_ij)是G中各弧上的权构成的矩阵，即W的元素w_ij是G中结点v_i到结点v_j的弧上的权（如果v_i到v_j无弧，则令w_ij=∞）。我们的目的是计算G中所有结点对之间的最短路。为此，记d_ij为结点v_i到结点v_j的最短路长，并记D=(d_ij)。用d_ij^k表示从v_i到v_j至多经过k-1个中间结点的所有路径的长度的最小值，记D^k=(d_ij^k) 。因此d_ij¹=w_ij（i≠j），d_ij¹⁼0。如果假设G中不包含权为负的有向圈，则d_ij=d_ij^n-1，D=D^n-1。

　　根据组合最优原理（Combinatorial Optimization Principle）有
　　　　　　　。

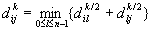　　从而可以从D¹开始，逐次计算出D²，D⁴，D⁸，…，D^n-1=D。为了从D^k/2计算D^k，可以借用标准的矩阵乘法。矩阵乘法执行的计算是
。
　　　　　　　
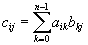
　　只需将矩阵乘法中的乘法操作换成加法操作，把矩阵乘法中的求和换"求最小值"操作即可。

　　小结 以上介绍的三种并行程序设计方法显然不能涵盖并行程序设计的全部。算法设计是很灵活而无定规可循的。以上介绍的三种方法只是为并行算法设计提供了三条可以尝试的思路。