|
由某个字符集中的字符组成的有限序列称为串或字符串。串中包含的字符的个数称为串的长度。给定长度为n的正文串T和长度为m的模式串P,找出P在T中所有出现的位置称为串匹配问题。目前已知的有效的串匹配算法均不易直接并行化。但是,参照串行算法的实质,结合使用串的周期数学性质,可以开发出有效的并行算法。第一个最优的并行串匹配算法是由Galil提出的。后来Vishkin改进了Galil的算法。Vishkin算法十分复杂,下面只介绍其思路。
研究发现,两串能否匹配是与串本身的特性有关的。这种特性,就是串的周期性。串可以分为周期的和非周期的。可以引入见证函数(Witness
Function)来判断串的周期性。确定了串的周期性后就可以先研究非周期串的匹配,然后在此基础上再研究周期串的匹配。
对于非周期串的研究,就是如何利用见证函数快速地找出P在T中的位置。为此,引入竞争函数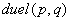 。先把正文串分成小段,借助于见证函数并行地计算竞争函数值,找出那些可能匹配的位置。然后逐步扩大正文串分段的长度,并计算竞争函数值,在可能匹配的位置中排除那些不可能匹配的位置。最后在剩下的可能位置中验证哪些是符合要求的位置。 。先把正文串分成小段,借助于见证函数并行地计算竞争函数值,找出那些可能匹配的位置。然后逐步扩大正文串分段的长度,并计算竞争函数值,在可能匹配的位置中排除那些不可能匹配的位置。最后在剩下的可能位置中验证哪些是符合要求的位置。
假设T=abaababaababaababaababa,n=23,P=abaababa,m=8。由见证函数可知P是非周期串。因为P只可能在前16个位置上与T匹配,所以在找所有"可能位置"时只考虑T的前16个字符。匹配时,先要计算见证函数值,然后由其计算
的值,找到可能匹配的位置。计算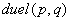 时,可以所有的块并行计算。先将P和T分成长度为2的块,用模式块(ab)
与正文块(ab)(aa)(ba)(ba)(ab)(ab)(aa)(ba)进行匹配可知模式块(ab)在位置1,4,6,9,11,14,16(即 时,可以所有的块并行计算。先将P和T分成长度为2的块,用模式块(ab)
与正文块(ab)(aa)(ba)(ba)(ab)(ab)(aa)(ba)进行匹配可知模式块(ab)在位置1,4,6,9,11,14,16(即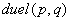 的获胜者)出现匹配。再把P与T划分成长度为4的块,用模式块(abaa)与正文块(abaa)(baba)(abab)(aaba)进行匹配可知在位置1,6,11,16出现匹配(位置4、9、14被淘汰);最后用模式串(abaababa)在正文串的位置1,6,11,16进行检查,排除那些不匹配的位置。本例中这4个位置都匹配。 的获胜者)出现匹配。再把P与T划分成长度为4的块,用模式块(abaa)与正文块(abaa)(baba)(abab)(aaba)进行匹配可知在位置1,6,11,16出现匹配(位置4、9、14被淘汰);最后用模式串(abaababa)在正文串的位置1,6,11,16进行检查,排除那些不匹配的位置。本例中这4个位置都匹配。
|