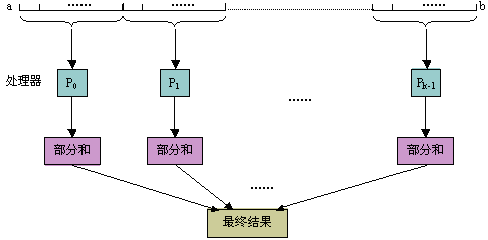
直接并行化已有串行算法时要注意两个问题：第一，并非所有的串行算法都可以并行化。某些串行算法有内在的串行性，比如在某些串行算法中，每一步都要用到上一步的结果。只有当上一步完全结束后，下一步才能开始。这样，各步之间就不能并行，只能考虑其它的并行化办法。例如模拟退火算法，每个温度下迭代的出发点是上一个温度下迭代的结束点。这样就很难直接将各个温度的迭代并行起来。第二，好的串行算法并行化后并不一定能得到优秀的并行算法；另一方面，不好的串行算法并行化后也可能是优秀的并行算法。例如，串行算法中是没有冗余计算的。但是在并行算法中，使用适当的冗余计算也可能使并行算法效率更高。加入冗余计算的并行算法就可能比直接由串行算法并行化得到的算法效率高。又比如，枚举不是一种好的串行算法。但是将其直接并行化后可以得到比较好的并行算法。

　　直接并行化的关键在于分析和暴露原有串行算法中固有的并行性。直接并行化也不是机械的，完全直接的。有时为了暴露算法的并行性，要对串行算法进行一些适当的改动。总之，要在保证算法正确性的前提下，尽量提高算法的效率。

　　假设我们想用求和的方法进行数值积分。设被积函数为f(x)，积分区间为[a,b]。为了积分，将区间[a,b]均匀分成N个小区间，每个小区间长，根据积分的定义
　　　　　　　　，
是第i个小区间左端点的坐标，而是f(x)在第i个小区间上积分的近似值。如果使用串行算法，可以用循环和叠加完成上述求和。这个串行算法可以直接并行化。假设有k台处理器，可以把这N个小区间上的计算任务分到各处理器：0号处理器负责第个小区间上的计算和累加，1号处理器负责第个小区间上的计算和累加，……，k-1号处理器负责第个小区间上的计算和累加。k个处理器并行地计算出部分和，然后再把结果加到一起。
　

　　科学和工程中有大量数值计算问题。针对这些问题，人们已经设计出了许多串行数值计算方法。在设计这些问题的并行算法时，大多采用串行算法直接并行化的方法。这样做的一个显著优点是，算法的稳定性、收敛性等问题在串行算法中已有结论，不必再考虑。