数据共享的交互

　　静态数据共享交互是指数据访问的模式在程序实际执行之前就可以完全确定的交互。比如，对矩阵乘法，我们在设计算法的时候就知道为了计算结果矩阵中的每个元素，需要访问源矩阵中的哪些数据，而不管它们的具体值是多少。而动态数据共享则是指数据的访问模式在计算前无法预先确定的交互。比如考虑考虑一个稀疏矩阵A和向量b的乘法Y=Ab，一种通常的分解方法是做输出数据分解。下面的图给出了一个分解的实例。
　　

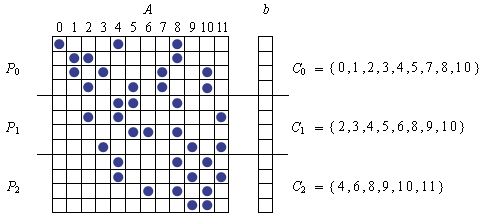
　　源数据被划分为三等分，这个例子中，即使我们可以知道每个任务需要访问A的那些列，我们也不知道这个任务实际需要b的那些元素。这是因为，对b的访问依赖于稀疏矩阵的结构，对不同的稀疏矩阵，它的访问模式也不同。

　　实际上，静态数据访问模式和数据的内容（问题的实例）无关，而动态数据访问模式则依赖于数据的内容。

　　另外一个可能出现动态数据访问模式的情形是非确定性算法的使用。这类算法的一个例子是那些依赖于随机数的算法。比如，求一个图G=(V,E)的最大不相关节点集（Maximal independent set of vertices, or MIS of vertices）I。不相关节点集是指这个集合中的任意两个节点都不相邻。最大不相关节点集则是指这个集合中不可能在不违反不相关条件的情况下包含任何其他的节点。Luby提出的算法如下：开始令I=θ(空集)，然后逐步加入节点直到产生最大不相关节点集。算法的主循环如下：
　　1． 为G的每个节点产生一个唯一的随机数；
　　2． 每个随机数比相邻节点的随机数大的节点被插入I；
　　3． 将插入I的节点和它的所有相邻节点从G中删除。

　　当G为空时，算法结束。由于使用了随机数，这个算法具有不确定性（指过程不确定）。
　　（思考，这个算法为什么可以得到正确的结果？）

　　这个算法可以通过对图进行划分的方法并行化，但我们可以看出，这个算法无法实现确定数据访问模式。

　　一般来说，表现出静态数据访问模式的算法要比较容易表达和优化，不管实际的系统结构和并行程序语言是什么，往往能够得到很高的效率。而具有动态数据访问模式的算法则难于表达和优化，很多情况下，它们的性能和底层的系统结构以及用于实现它们的并行程序语言有关。实际上，对动态交互来说，程序员必须显式地给出一个"交互探索"过程，也就是说，程序需要动态地确定它需要访问哪些数据。在共享存储的系统结构上，表达静态和动态数据访问模式都要简单许多。