图的分割策略

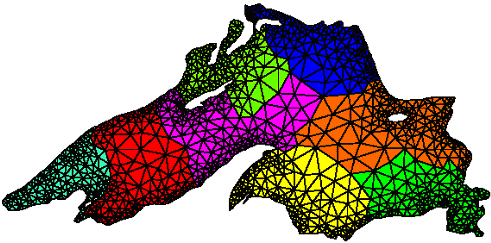
　　上面介绍的面向数组的分布策略对那些对稠密矩阵进行运算，交互模式十分规则的数据并行算法非常有效。但很多的算法中的数据结构是稀疏矩阵，而且数据元素之间的交互模式十分不规则。实际的应用中，物理现象的数值模拟有很多都是这类的算法。在这些计算中，物理域通常被离散化，并被表示为元素的网格。计算在每个格点上进行，它们只和网格中相邻的一些格点有关。比如，为了对湖水的污染进行模拟，会使用下图中的网格，并使用这个网格来进行污染扩散的数值模拟。


　　通常情况下，每个格点处的所进行的计算量都相同，所以只要我们给每个处理器分配相同数量的网格点，那么负载很容易平衡。但是，这样的对网格点的简单分布会导致高昂的数据共享开销，因为这样的分布并不会试图将相邻的网格点分配到一起。比如，我们将网格点在处理器上随机分布，如下图表示的一样（不同的颜色表示分配到不同的处理器），这会保证每个处理器分配到相同数量的网格点（同时也意味着它们的任务量相同，即负载平衡），但每个处理器为了完成计算，都需要访问大量的相邻的网格点，而这些格点不一定会是本地的，所以需要大量的处理器间的交互，这会带来非常大的额外开销。


　　理想情况下，在分布网格点时，我们应该在平衡负载的同时，同时尽量减少每个处理器为了完成计算所需要访问的数据量。可以用图划分的方法来达到这个目标。我们用图来表示上面的计算。计算被表示为图G=(V,E)，其中，图中的每个节点u∈V对应于算法中的计算，而图中的边e∈E表示它连接的两个节点间的依赖关系。也就是说一条边（u,v）表示为了计算u，需要从节点v得到某些信息，这也就意味着节点u和v代表的任务需要某些交互。由于每个节点只需要与相邻的节点进行交互，因此G是一个稀疏图。这时我们可以采用图划分算法来将G划分为p个部分，划分要求每个部分有相同数量的节点（负载平衡要求），同时，连接每个部分间的边数最少。最后，这p个部分被分别分配给p个处理器。上面的例子的一个合适的划分如下图所示：