|
数组分步策略
块分布
当数组的每个元素相关的计算是均衡的时候,我们可以采用简单的块分布策略:为每个处理器分配相同数量的数组元素。在这种分布策略下,一个d维的数组按块分布到每个处理器上,每个处理器上的数组在某些特定的维上是连续的块。比如,一个二维数组A(可以把它看成一个矩阵),每维的大小为{n1,n2}。我们可以选择其中的一维,比如第一维,把数组在这一维上分成p个块(p为处理器数目),这样,第k个处理器上分到得数组为ai,j,其中有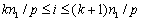 ,且 ,且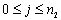 。如果我们把数组的第一维看成数组的行,那么每个块包含A的n1/p个连续行,这称为按行分布(row-wise
distribution)。相似的,选择在第二维上进行分块,那么每个块包含A的n2/p个连续列,这称为按列分布(column-wise
distribution)。参见下面的图: 。如果我们把数组的第一维看成数组的行,那么每个块包含A的n1/p个连续行,这称为按行分布(row-wise
distribution)。相似的,选择在第二维上进行分块,那么每个块包含A的n2/p个连续列,这称为按列分布(column-wise
distribution)。参见下面的图:
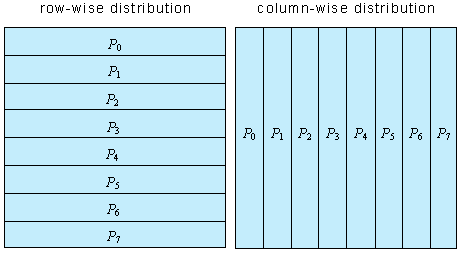
同样的,我们也可以选择多个维进行块划分,比如上面的数组A,我们可以同时对两个维进行块划分:划分后,每个块包括了原来数组的n1/p1×n2/p2之一,其中p1×p2等于处理器的数目。下面的图给出了两种不同的二维块划分,分别对应4×4和2×8的处理器网格。一般来讲,对d维数组,我们最多能对它进行d维的块划分。
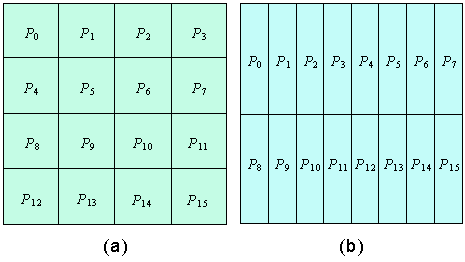
块分布的策略对主要在多维数组上进行的计算任务的分布非常有效(事实上,很大一部分的科学计算都属于这一类)。比如n×n的矩阵乘法C=A×B
。前面曾经讨论过按C进行输出数据划分,由于C的每个元素需要相同量的计算,所以我们可以对C进行一维或二维的块分布。一维分布时,每块包含C的n/p行(列),对二维分布,块的大小为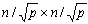 。 。
|