举这样一个例子的目的是想说明有些问题采用递归分解或数据分解的方法并不总是有效，对上面的例子，一个更好的分解方法如下：首先把数据库划分为相等的部分（划分数与我们需要找出的客户数量无关），然后对每个部分的纪录进行随机排列，然后对每个子数据库进行并行扫描，每次找到一个高价值客户，把它记录下来，并用一个全局计数器对目前找到的高价值客户数目进行记录。当全局计数器到10时，所有的搜索过程结束。

　　这个例子中给出的方法被称为搜索分解方式（exploratory decomposition），因为这种分解方法通常用于那些需要对解空间进行搜索的问题。在这种分解方式下，我们把搜索空间分成小块，然后对每个块进行并行搜索，直到找到需要的解。虽然看起来搜索分解方式与数据分解看起来一样（搜索空间可以被看作被划分的数据），但我们可以找到下面的不同点：

　　数据分解得到的任务分解是独立的，每个任务所进行的任务都是确定的，每个任务所进行的计算都会对最后的结果有所贡献；而对搜索分解来说，所有的子任务"合作"完成工作，只要最后答案找到了，所有没有完成的任务也就终结了。因此，和串行算法相比，并行搜索算法所搜索的空间非常不同。

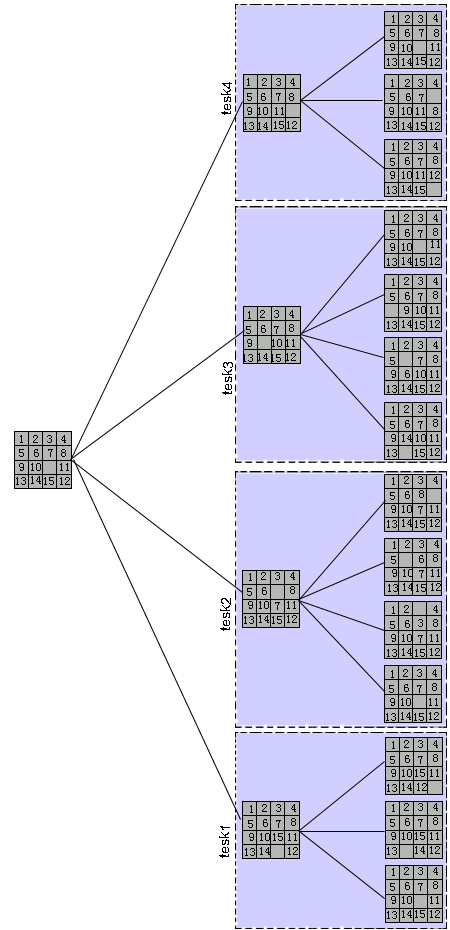
　　为了说明搜索分解，我们来看下面熟悉的例子。这个例子是一个拼图游戏（15-puzzle problem）。问题说明如下：一个 的网格，包含了16个相同大小的方块，其中15个方块有标号，从1到15，各不相同，另有一个空的方块。游戏的规则如下：与空方块相邻的标号方块i可以移到空方块的位置（原先空方块的位置被标上标号i，原来i所在的位置成为空方块）。除了边界外，方块只有四种可能的移动方向：上，下，左，右（当然需要满足上面的空方块的要求）。游戏的网格初始状态和终结状态给处，游戏的目标是找出一个对方块进行移动的序列，以使网格能从初始状态到达终结状态。下面的图给出了一个可能的游戏过程。
　　 　　　　 　　

　　这个游戏通常用搜索树的方法来解决。从最初的格局出发，所有可能的变化被产生。一个给定的格局可能有2，3或4个可能的后继格局（和空方格所在的位置有关）。这样会产生一棵搜索树，原先的问题变成了在树中找一条从根结点到最后格局节点的（最短）路径。

　　为了并行的解这个问题，我们可以先串行的产生搜索树的几层，直到有了足够的叶子节点。比如，从初始状态（根节点）出发，最多可以产生4个子节点，这些节点可以继续扩展来产生更多的节点。（当然产生的过程为了避免出现格局的重复，并不是每一种格局都会被产生）继续这个过程，直到产生足够数量的子节点。这时，这些子节点可以分配给多个处理器，作为它们搜索的起点。搜索过程的结束与对解的要求有关，比如如果只需要找到一个可能的解（而不是最短路径的解），那么第一个找到解的任务就可以马上通知其它的任务结束。而如果我们需要寻找一个最优解（比如最短路径的解），那么此时所有的子任务都需要穷尽搜索空间（或者它能够确定找到的解就是最优解）的时候才能结束。这个过程可以参见下面的图：