对输入数据进行划分

　　前面讨论的两种数据划分方法实际上都是对输出数据进行划分，能进行这种划分的一个前提是每个输出都可以被自然的表示为输入数据的函数。对很多算法，这个条件并不一定能满足，比如对一个排序算法，输出的每个元素的位置不能被（有效的）独自确定。这种情况下，由于无法对输出数据进行划分，有时可以尝试对输入数据进行划分，然后根据这个划分来得到并行任务集。每个并行子任务在（自己的）数据（或称为本地数据）上进行尽可能多的计算。需要注意的是，这些并行任务集给出的计算结果也许还不是原来问题的答案，因此，常常还需要一个计算阶段来根据这些结果来生成最后的答案。

　　考虑前面讨论过的快速排序算法。快速排序算法一个重要步骤是选定一个序列中的一个元素作为轴元素（pivot），然后对序列进行划分，划分后一个子序列包含所有比轴元素小的元素，而另外一个子序列包含比轴元素大（或等于）的元素。现在考虑如何来完成这个步骤。假设序列是一个n个元素的数组，为了简化讨论，我们假设挑选的轴元素在数组中是唯一的（即它的值与其它的数组元素的值都不同）。下面的图给出了一个实例（n=16）。5被选为轴元素（这个选择本身所用的算法我们在此不做讨论）。左边是算法输入，右边是算法输出（都是一个单一的数组）。现在考虑这个问题的解决方法。为了得到结果序列，输入数组的每个元素需要和轴元素进行（独立的）比较，然后需要计算出比轴小的元素的数目以及比轴大的元素的数目，这样，轴元素在输出数组中位置（数组下标）就确定了，其余的元素可以很简单的从输入数组拷贝到输出数组。
　　　　　　　　　

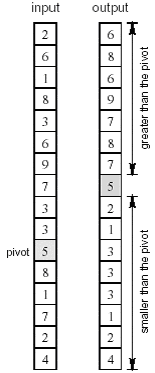
　　上面的算法不可能使用对输出数据进行划分的方法：因为输出序列中的每个元素的下标不能根据输入序列（注意，有可能，但并不高效）单独计算。但这个算法可以通过对输入数据划分的方法来开发并行性。这种划分的细节可以参考下面的图。16个元素的数组被均匀的划分成4个子序列（以分配给4个处理器并行处理）。


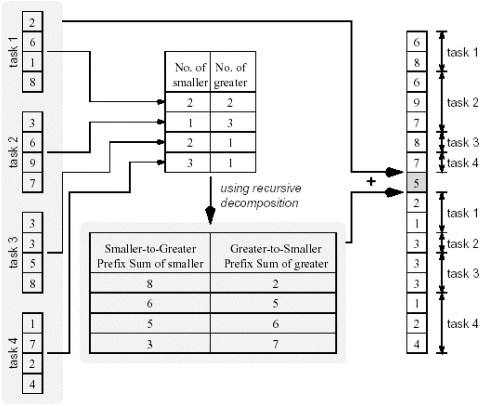
　　算法包括三个阶段。第一阶段每个处理器将自己的序列中的各元素与轴元素进行比较，得到本地序列中比轴元素小的元素数目和大于等于轴元素的元素数目。第二个阶段中采用递归分解的方法来对上面的数据计算前序和（注意计算小元素数目和大元素数目的方向不同）。第三个阶段中每个处理器根据自己本地的前序和（实际上给出了输出数组的下标），来将本地的元素拷贝到输出数组中。

　　对有的算法，虽然可以采用按输出数据进行划分的方法，但在此基础上对输入数据进行划分也许可以提供额外的并行化途径。考虑下面的例子：计算一个事务数据库中某个项目集出现的频率。事务集T包含n个事务，项目集I包含m个子项目集（I= I1，I2，...，Im）。每个事务和项目集由一些项目组成，这些项目都包含在一个可能项目集M中。计算的输出是对每个项目集I_i，计算出它在所有的事务中出现的总次数。下面的图给出了一个计算的实例。
　　　　　　

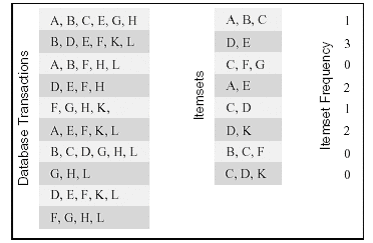
　　这个例子中数据库包括10个事务，而我们感兴趣的项目集有8个，计算结果为每个项目集在事务中出现的总次数。比如，项目集{D,E}在事务{B,D,E,F,K,L}，{D,E,F,H}，{D,E,F,K,L}中出现，所以，它的出现频率为3。

　　实际上，这种类型的计算是数据挖掘问题的一个必需的步骤，称为关联规则发现（association rule discovery）。解决这个问题的串行算法会为I中的子项目集建立一个查找结构（比如哈希树），然后对T中的每个事务，它会穷举所有的可能的项目组合，看能否和I中的任何项目集相匹配。比如，对于事务{A,B,C}，算法可能构造的项目集包括{A}，{B}，{C}，{A,B}，{A,C}，{B,C}，{A,B,C}(实际上是事务的幂集除去空集)，然后看它们是否在查找结构中存在。如果找到一个匹配，就把对应的频率计数器加1。使用查找结构的目的是为了使匹配的过程更加高效。

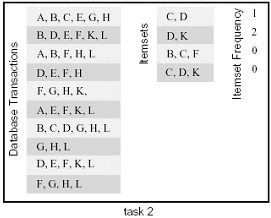
　　在这个算法中，有两个输入T，I和一个输出数组。它们都可以用来对算法进行划分。比如，我们可以对T进行划分：把它分成两个相同大小的子集，分别进行计算，然后对最后的结果进行组装。如下图所示：
　　　　　　
　　　　　　

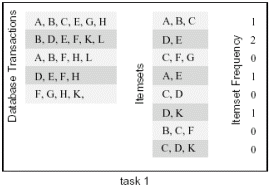
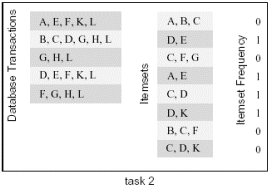
　　另外一种可行的数据划分方法是对项目集I进行划分：把I划分为两个相同大小的部分，它们可以独立的计算出自己的频率。（需要注意的是，对输出数据进行划分的结果和这种划分得到的结果相同，因为项目集和频率是一一对应的关系）。